Posted on by Bill

Does the Square Root of Two Exist?

The proof that the square root of two is an irrational number is considered to be one of the most elegant in all of mathematics.

As a formal “If…, then…” statement, it reads: If x^{2}=2, then x is not a rational number. A more informal statement of this is “the square root of two is irrational”.

Rational Numbers

But what is a rational number? A rational number is a number that can be represented as a fraction (ratio) where the numerator (top) and denominator (bottom) are integers (\ldots,-3,-2,-1,0,1,2,3,\ldots), and the denominator is nonzero. For example, 3.14 is a rational number since 3.14=\frac{314}{100} (careful: this is NOT the same as “pi” \pi).

Notice that the fraction above can be “reduced”: \frac{314}{100}=\frac{157\cdot 2}{50\cdot 2}=\frac{157}{50}, where the “2’s” have been “cancelled”. The fraction \frac{157}{50} can no longer be reduced because 157 and 50 have no common (integer) factors. In fact, 157 is a prime number. Therefore, the representation of a rational number as a fraction is not unique. It also turns out that any given representation as a fraction can always be completely reduced until the numerator and denominator have no common factors.

The Proof that the Square Root of Two is Irrational

Below is an elegant proof of the “If…, then…” statement above. It was discovered by the ancient Greeks over 2000 years ago. It is elegant because it proves this very profound fact in a relatively brief way with an ingenious strategy.

The profundity of this fact supposedly had an unfortunate real-world consequence. There is a story that Hippasus of Metapontum was killed for discovering it because it went against the worldview of the Pythagoreans.

The ingenious strategy used is a proof by contradiction.

Proof: Suppose x is a number with the property that x^{2}=2. Suppose, for the purpose of obtaining a contradiction, that x is rational (the opposite of what we want to prove). Then there are integers p and q, which have no common factors, such that x=\frac{p}{q}. Since p and q have no common factors, at least one of them must be an odd number.

Since x^{2}=2, we can say that \frac{p^{2}}{q^{2}}=\left(\frac{p}{q}\right)^{2}=2. Thus, p^{2}=2q^{2}. But this means that p^{2} is even and therefore p is even — say p=2r for some integer r. (Think about it: if p were odd, then p^{2} would also have to be odd.)

Plugging this into the equation p^{2}=2q^{2} leads to 4r^{2}=(2r)^{2}=2q^{2}. This implies that q^{2}=2r^{2}. But then q^{2} is even, leading to the conclusion that q is even.

Therefore, we conclude that p and q are both even. This contradicts the fact that we said at least one of them is odd. This means that our original assumption that x is rational must be false. It must in fact be irrational. We are done. Q.E.D.

Related Video

The fact and proof given above are special cases of the fact and proof given in the video embedded below. In this video, it is proved that, if n is a positive integer which is not a perfect square, then \sqrt{n} is irrational. The Fundamental Theorem of Arithmetic is required to prove this.

Proof that the square root of a non-perfect square is irrational. The Fundamental Theorem of Arithmetic is required to do the proof.

But Does the Square Root of Two Really Exist?

The proof that the square root of two is not rational makes an implicit assumption: that the square root of two exists. That is, we are assuming that there is a number x such that x^{2}=2.

But is it possible that there is no such number?

This is definitely a harder question to answer. Geometric reasoning seems to indicate that there must be such a number. After all, according to the Pythagorean Theorem, if a square has side length 1, its diagonal must have length c, where c^{2}=1^{2}+1^{2}=2. See the figure below. In other words, the length of the diagonal must be the square root of two.

The square root of two as the length of the diagonal of the unit square.
For a square whose sides have length 1, the diagonal must have length \sqrt{2}, by the Pythagorean Theorem.

Doesn’t the diagonal of a square indeed have a length? Isn’t the Pythagorean Theorem true? We don’t want the foundation of everything we learned about geometry to crumble — do we?

The Arithmetic Standpoint

While the existence of \sqrt{2} seems irrefutable from this geometric standpoint, it is not irrefutable from a purely arithmetic standpoint (as an adjective, pronounce “arithmetic” as: eriTHˈmedik).

If we think about rational numbers either as fractions or in terms of their decimal representations (which either terminate or have an infinitely repeating pattern), we know by the proof above that we will never come up with a rational number whose square is two. How then can we know that there is some infinite non-repeating decimal representation of a number whose square equals two, exactly?

By trial-and-error, we could keep finding terminating decimal expansions whose squares gets closer and closer to two. For example, 1.41421356^{2}=1.9999999932878736 and 1.414213562^{2}=1.999999998944727844.

But this method is no good! This approximation process will never stop! And how in the world would we square an infinite non-repeating decimal anyway? Yikes! We need another approach.

What We Need Instead

The approach we need is part of the subject called Real Analysis. In this subject, the emphasis is on the arithmetic viewpoint, because humans can be more easily misled by pictures. But it also uses pure logic rather than a computational/approximation strategy.

The research program for doing this from the ground up in the 19th century was called the arithmetization of analysis. Its effects are with us in strong ways today. Advanced Real Analysis, sometimes referred to as “Measure Theory and Integration“, has profound implications and applications. These include, for example, applications in Probability, Physics (Quantum Mechanics), and Finance & Economics.

Constructing the (Positive) Square Root of Two

Truth be told, the approach taken to prove that the square root of two exists is to mathematically “construct” it. This means that precise language and logic are used to “create” a number system that has a mathematical “object“, or “entity”, whose square is two.

This can actually be a ton of work, depending on your starting point. As an extreme example, in the tome “Principia Mathematica“, written in the early 20th century by Alfred Whitehead and Bertrand Russell, it takes 379 pages to prove that 1 + 1 = 2!

The task of thinking deeply about what is really going on when such a thing is done is the realm of the philosophy of mathematics. In this field of study, we can ask, and attempt to answer, questions such as: Do mathematical objects really exist? Is mathematics discovered or created? Sometimes such questions are even pondered in relation to faith in God.

Our Mathematical Construction

Interesting as this subject is, in this article, we will focus on the mathematical construction. But is there a way we can construct the square root of two more quickly than Whitehead and Russell did?

The answer is yes — though what we will do might feel like “cheating”.

First Assumption

We will do this by assuming, first of all, that all rational numbers have already been constructed and that we already understand the arithmetic and algebra of rational numbers.

To be more thorough here, we would actually need to spend time discussing the mathematical concept of a “field“. It will suffice for us to say that, in a field, all the abstract algebraic properties you learned in school, such as the distributive property, work as you would expect.

Second Assumption

Secondly, we will also assume that we fully understand the concepts of “greater than” and “less than”, and their cousins “greater than or equal to” and “less than or equal to”. This includes understanding the relationships between these concepts and the arithmetic operations of addition and multiplication. For example, we will assume that we already know that the product of two positive numbers (two numbers greater than zero) is also positive; and that the product of a positive number and a negative number is negative. We will also assume, for example, that if a<b and c>0, then ac<bc.

As was discussed in the post “Deconstructing the Mean Value Theorem, Part 2“, there is one more thing we need to assume: the Completeness Axiom. This will be something that is assumed to be true about all real numbers. In other words, we will assume that the real numbers are an ordered field that satisfies this axiom and go about constructing the square root of two from that point.

Statement and Meaning of the Completeness Axiom

The Completeness Axiom can be stated in a precise way as follows:

Completeness Axiom: Let S be any nonempty set of real numbers that is bounded above, so that there is a real number M such that x\leq M for all x\in S. Then there is a real number \beta with the following properties: 1) x\leq \beta for all x\in S (\beta is an “upper bound” of S) and 2) if y<\beta, then there is a number x\in S so that y<x (any real number less than \beta is not an upper bound of S). The number \beta is called the (unique) least upper bound of S. It is also called the supremum of S and we write \beta=\sup(S).

This is quite a mouthful and you really need to consider examples to understand it. But at the moment let us just remark that \beta=\sup(S) is kind of like a maximum value of the set S, though it might NOT actually be a member of S! As a simple example, if S is the open interval (0,1), then 1=\sup(S), but 1\not\in S.

Now we construct the square root of two as follows: let S be the set of all real numbers whose square is less than two, symbolically, S=\{x\in {\Bbb R}:x^{2}<2\}. We claim that the supremum of this set is the square root of two. If you think about graphing S as a set on a number line, this claim should make intuitive sense. However, this claim takes proof.

Proof that the Supremum of S is the Square Root of Two

What is the first thing that must be proved? Well, in order to even have a real number supremum, this set must be nonempty and bounded above. Clearly S is nonempty since, for example, 1\in S.

Can we think of a possible upper bound? How about M=2? This seems like it should work. Can we prove it? Let us argue by contradiction: suppose, to the contrary, that M=2 is not an upper bound of S=\{x\in {\Bbb R}:x^{2}<2\}. This would mean that there is a number x\in S with x>2=M. But then (assuming we know properties of inequalities) we can say that x^{2}>2^{2}=4, contradicting the fact that x^{2}<2<4 since x\in S. Hence, S is bounded above.

The Completeness Axiom now can be invoked to say that \beta=\sup(S) exists as a real number (note also that \beta>0 since 1\in S). There is only one thing left to prove: that \beta^{2}=2. But how in the world can this be done?

Showing 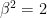\beta^{2}=2 by Contradiction and the Law of Trichotomy

We can again use an argument by contradiction (we are seeing that this is a very useful method of argument). Suppose, to the contrary, that \beta^{2}\not=2. The so-called “Law of Trichotomy“, which we can use since we are assuming we fully understand inequalities, then leads to the conclusion that either \beta^{2}>2 or \beta^{2}<2. Though the rest of the argument is tricky, we will see that both of these statements lead to logical contradictions, ultimately implying that \beta^{2}=2.

The Case Where \beta^{2}>2

What happens if, for example, \beta^{2}>2? Intuitively, by “continuity“, we might hope that there is a number slightly less than \beta whose square is also greater than 2. But this would imply that the number slightly less than \beta is an upper bound of S, which would contradict the fact that \beta is the least upper bound of S.

Let’s do some scratch-work to figure out the details: how small should \delta>0 be so that, if \beta^{2}>2, then (\beta-\delta)^{2}>2 as well?

Start by computing (\beta-\delta)^{2}=\beta^{2}-2\beta\delta+\delta^{2} and notice that this is greater than \beta^{2}-2\beta\delta (since \delta^{2}>0). We can now rephrase our question as: how small should \delta>0 be so that, if \beta^{2}>2, then \beta^{2}-2\beta\delta>2?

Solve this last inequality for \delta: adding 2\beta\delta to, and subtracting 2 from, both sides gives 2\beta\delta<\beta^{2}-2. Now divide both sides by the positive number 2\beta to get \delta<\frac{\beta^{2}-2}{2\beta}. Since \beta^{2}>2, the right-hand side of this inequality is a positive number, so a \delta>0 satisfying this inequality can be “found” (actually, this last statement takes proof as well).

Reversing the Logic

To make the argument prove what we really want it to prove, just reverse the logic: since \beta>0 and \beta^{2}-2>0, we can choose a number \delta>0 satisfying 0<\delta<\frac{\beta^{2}-2}{2\beta}, implying that 2\beta\delta<\beta^{2}-2 and \beta^{2}-2\beta\delta>2. But this means (\beta-\delta)^{2}=\beta^{2}-2\beta\delta+\delta^{2}>\beta^{2}-2\beta\delta>2, so that \beta-\delta is an upper bound of S (think about this!), contradicting the fact that \beta=\sup(S) is the least upper bound of S.

The Case Where \beta^{2}<2

Therefore, the option \beta^{2}>2 is ruled-out. What about \beta^{2}<2?

Again, by continuity, we might hope there is a number \delta>0 so that (\beta+\delta)^{2}<2 as well. If this happens, it would contradict the fact that \beta is an upper bound of S, because it would imply that \beta<\beta+\delta\in S.

We again start with scratch-work: first, compute (\beta+\delta)^{2}=\beta^{2}+2\beta\delta+\delta^{2}. If we assume, for the sake of argument, that 0<\delta<1, then we can say that 0<\delta^{2}<\delta<1, so that (\beta+\delta)^{2}<\beta^{2}+(2\beta+1)\delta. We want to choose \delta>0 so that this last expression is less than 2. Solving the inequality \beta^{2}+(2\beta+1)\delta<2 for \delta gives \delta<\frac{2-\beta^{2}}{2\beta+1}. Since 2-\beta^{2}>0 and 2\beta+1>0, a positive solution for \delta exists.

Reversing the Logic

Now reverse the logic. Assume that \beta^{2}<2 so that 2-\beta^{2}>0. Since 2\beta+1>0, we can choose a number \delta>0, with \delta<1, satisfying \delta<\frac{2-\beta^{2}}{2\beta+1} (so 0<\delta<\min\{1,\frac{2-\beta^{2}}{2\beta+1}\}).

This implies that (2\beta+1)\delta<2-\beta^{2} and \beta^{2}+(2\beta+1)\delta<2. But 0<\delta<1, so that 0<\delta^{2}<\delta<1, which means (\beta+\delta)^{2}=\beta^{2}+2\beta\delta+\delta^{2}<\beta^{2}+(2\beta+1)\delta<2. This contradicts the fact that \beta is an upper bound of S.

Therefore, the option \beta^{2}<2 is also ruled-out.

We are happily forced to conclude that \beta^{2}=2. We are done. Q.E.D.

Concluding Thoughts

The algebra and logic of this proof can certainly be confusing. Even if you follow every step, however, it may still feel unsatisfying. Have we really “constructed” \sqrt{2}?

According to the Completeness Axiom, yes, we have. The number \sqrt{2} is constructed to be the supremum of a certain nonempty set of real numbers that is bounded above.

But what about the truth of the Completeness Axiom itself?

The fact we are calling this property an “axiom” is a big hint that we are using it as a starting point — in actuality, by assuming that it is true.

But is that “fair”?

It depends on your point of view. All of mathematics takes place in the framework of some “axiomatic system“. We need a starting point to avoid implicit assumptions and/or circular reasoning. The choice of axioms that we work with is, to some extent, a matter of taste. As Whitehead and Russell did, we could start with much more “foundational” or “rudimentary” axioms and go from there, though that would make our task much more arduous.

If we chose more rudimentary axioms, the Completeness Axiom would no longer be an axiom. It would instead be a theorem that would require proof.

Other Ways of Constructing the Real Numbers

If you are interested in other ways to construct the real number system, prove completeness, and prove that objects like \sqrt{2} and \pi exist, you might consider, as a starting point, the Wikipedia page https://en.wikipedia.org/wiki/Construction_of_the_real_numbers.

We end by emphasizing that the existence of the particular root \sqrt{2} is a very special fact, and it is not as important as the existence of a general (positive) nth root \sqrt[n]{b} of an arbitrary real number b>0.

The Completeness Axiom can be used for such a general proof. A rigorous reference to find a proof is the so-called “baby Rudin” textbook: https://www.amazon.com/Principles-Mathematical-Analysis-International-Mathematics/dp/007054235X.