The Archimedean Property - Infinity is Really Big

The Completeness Axiom is a sufficient condition to prove the Archimedean Property, but is it necessary?

Real Analysis Study Help for Baby Rudin, Part 1.5

*A Visualization of the Archimedean Property in the case where $x=8$ and $y=70$ . The smallest positive integer value of $n$ that makes $nx>y$ is $n=9$ .*

*A Visualization of the Archimedean Property in the case where $x=8$ and $y=70$ . The smallest positive integer value of $n$ that makes $nx>y$ is $n=9$ .*

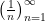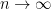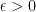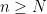Does the sequence $\left(\frac{1}{n}\right)_{n=1}^{\infty}$ approach zero as $n\rightarrow \infty$ ? Sure! After all, given any number $\epsilon>0$ , we can find a natural number $N\in \Bbb{N}$ such that $0<\frac{1}{n}<\epsilon$ for all $n\geq N$ . But are we “jumping the gun” here? Can we truly find such an $N$ ?

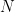The Archimedean Property is the name of the fact that allows us to be sure that we can find such a natural number $N$ . But what is the Archimedean Property? What does it state? Is it a theorem or an axiom?

The answer to this last question is somewhat a matter of taste, but it is traditional to take the Archimedean Property as a theorem.

In this fifth article on Real Analysis study help for Baby Rudin, we take a look the Archimedean Property, with a particular focus on how it can be proved using the completeness property of the real numbers. We will also need to review the definition of an ordered field. Along the way, we will have the opportunity to consider examples of field extensions.

The Archimedean Property and its proof can be found on page 9 of the third edition of Baby Rudin.

Ordered Fields and The Completeness Axiom

The briefest way to describe the set real numbers $\Bbb{R}$ is to say that is a complete ordered field. In fact, “up to isomorphism“, $\Bbb{R}$ is the unique complete ordered field. Any other complete ordered field must be essentially “the same” as $\Bbb{R}$ . That other field may be mathematically constructed in a different way, but it “acts” the same as $\Bbb{R}$ .

But what does all this mean?

Fields and Ordered Fields

In a nutshell, a field is an algebraic structure with two binary operations (typically some form of addition and multiplication) which is as “nice” as can be. It satisfies all the standard properties we could hope for: closure, associativity, commutativity, and distributivity. In addition (pun intended), there is an additive identity (a “zero”) and there are additive inverses for all elements. There is also a multiplicative identity (a “one”) and there are multiplicative inverses for all nonzero elements.

An ordered field is a field which is not only a totally ordered set, but which also has the property that the order is “compatible” with the field operations (see Study Help for Baby Rudin, Part 1.2, “Definitions of Ordered Set and Ordered Field”). In particular, any inequality is preserved under addition: $y<z\implies x+y<x+z$ . Furthermore, the product of any two positive elements is also positive: $x>0\mbox{ and }y>0 \implies xy>0$ .

The Ordered Field of Rational Numbers

The set of rational numbers $\Bbb{Q}=\left\{\frac{m}{n}\ |\ m,n\in \Bbb{Z}\mbox{ with }n\not=0\right\}$ forms a field under ordinary addition and multiplication of fractions. In other words, this is a field when we define $\frac{a}{b}+\frac{c}{d}=\frac{ad+bc}{bd}$ and $\frac{a}{b}\cdot \frac{c}{d}=\frac{ac}{bd}$ .

The rationals $\Bbb{Q}$ becomes an ordered field when we define $\frac{a}{b}<\frac{c}{d}$ to be true if and only if $\frac{d}{c}+\frac{-a}{b}=\frac{bd-ac}{cd}>0.$ In turn, this is true if and only if $bd-ac$ and $cd$ have the same sign (they are either both positive or both negative). Alternatively, if, without loss of generality, we choose $b>0$ and $d>0$ , we can define $\frac{a}{b}<\frac{c}{d}$ to be true if and only if $ad<bc$ (think about this in terms of cross-multiplication where the inequality stays the same direction).

The Ordered Field of Rational Numbers Adjoin Square Root of Two

As discussed in Study Help for Baby Rudin, Part 1.2, “Definitions of Ordered Set and Ordered Field”, the set $\Bbb{Q}(\sqrt{2})=\left\{a+b\sqrt{2}\ |\ a,b\in \Bbb{Q}\right\}$ is also an ordered field. It is certainly a field. Note, in particular, that if either $a\not=0$ or $b\not=0$ , then we can compute $\frac{1}{a+b\sqrt{2}}$ . In fact, $\frac{1}{a+b\sqrt{2}}=\frac{a-b\sqrt{2}}{a^{2}-2b^{2}}=\frac{a}{a^{2}-2b^{2}}+\frac{-b}{a^{2}-2b^{2}}\sqrt{2}$ . This can be computed because $a^{2}-2b^{2}\not=0$ since $a,b\in \Bbb{Q}$ with either $a\not=0$ or $b\not=0$ , and since $\sqrt{2}\not\in\Bbb{Q}$ . (Rest assured, however, that $\sqrt{2}$ exists.)

As we also saw in Part 1.2 linked in the paragraph above, there are actually two distinct (non-isomorphic) orders that make $\Bbb{Q}(\sqrt{2})$ an ordered field. We won’t go into the details here. Suffice it to say that from here on out we will assume that $\Bbb{Q}(\sqrt{2})$ has its “standard” order. This is the order it inherits as a subfield of the ordered field $\Bbb{R}$ of real numbers.

The Ordered Field of Real Numbers

But this begs a question. How do we define an order on $\Bbb{R}$ to make it an ordered field?

This is a point at which Baby Rudin, except in the appendix to Chapter 1, essentially takes an axiomatic approach. In fact, most textbooks in Real Analysis do this.

In other words, we do not describe how to define an order on $\Bbb{R}$ that makes it an ordered field. Nor do we prove that it is an ordered field. Instead, we just assume it is an ordered field and work from there.

This may seem like “cheating”, but we have to start somewhere. It is certainly a big time-saver.

Intuitively, the best way to describe the order on $\Bbb{R}$ is by considering examples using decimal representations of real numbers. For example, we say that $4.32771382\ldots < 4.32771392\ldots$ because the first real number has a smaller digit in the 7th place after the decimal than the second real number does (in spite of the fact that we do not know what the digits are in the 9th place after the decimal and beyond).

But this is just intuition that is trusting in your past education. We do not take the time to make this fully precise.

The Completeness Axiom of the Real Numbers

Technically, the completeness property (a.k.a. least upper bound property) of the real numbers is proved in Baby Rudin, though it is in the appendix of Chapter 1. In the appendix, the concept of a Dedekind cut is used to mathematically construct the real numbers and prove that it is a complete ordered field.

We may or may not take the time to delve into the appendix in future articles. But at this point, it does not matter. We are essentially taking an axiomatic point of view with regard to completeness — that is, we will take it to be an axiom that is assumed to be true for $\Bbb{R}$ .

Least Upper Bound (Supremum) and Completeness

First, we review a couple background definitions.

Recall the following definition from Study Help for Baby Rudin, Part 1.3, “Least Upper Bound (Supremum) in an Ordered Set”. If $S$ is an ordered set and $E$ is a nonempty subset of $S$ which is bounded above, then $\beta\in S$ is the supremum (least upper bound) of $E$ if: (i) $x\leq \beta\ \forall\ x\in E$ and (ii) if $\gamma<\beta$ , then $\gamma$ is not an upper bound of $E$ . In this case, we write $\beta=\sup(E)$ .

An ordered set $S$ is then said to have the least upper bound property (a.k.a. “is complete”) if every nonempty subset of $S$ which is bounded above has a supremum in $S$ .

As illustrated in the main example of Study Help for Baby Rudin, Part 1.1, “Baby Rudin: Let Me Help You Understand It!”, the field of rational numbers $\Bbb{Q}$ does not have the least upper bound property ( $\Bbb{Q}$ is not complete).

Here then, is the Completeness Axiom (labeled as Theorem 1.19 on page 8 of the 3rd edition of Baby Rudin, and proved in the Appendix of Chapter 1).

Completeness Axiom: There exists an ordered field $\Bbb{R}$ (the real numbers) which has the least upper bound property. Moreover, $\Bbb{R}$ contains $\Bbb{Q}$ (the rational numbers) as a subfield.

As stated in Baby Rudin, the second sentence means $\Bbb{Q}\subseteq \Bbb{R}$ with the same field operations (which match the field operations on $\Bbb{Q}$ described above in terms of ratios of integers). Furthermore, the positive rational numbers are also positive real numbers.

The Completeness Axiom and the Archimedean Property

What now does the Archimedean Property say? And how can it be proved with the Completeness Axiom? Here is how it is stated as part (a) of Theorem 1.20 in Baby Rudin.

Archimedean Property of $\Bbb{R}$ : If $x,y\in \Bbb{R}$ and $x>0$ , then there exists a positive integer $n\in \Bbb{N}$ such that $nx>y$ .

Certainly this is trivially true if $y\leq 0$ . In the case where $y>0$ , it can be visualized as shown in the animation below with $x=8$ and $y=70$ . The smallest positive integer value of $n$ that makes $nx>y$ is $n=9$ .

A visualization of the Archimedean Property. — A Visualization of the Archimedean Property in the case where $x=8$ and $y=70$ . The smallest positive integer value of $n$ that makes $nx>y$ is $n=9$ .

A Visualization of the Archimedean Property in the case where $x=8$ and $y=70$ . The smallest positive integer value of $n$ that makes $nx>y$ is $n=9$ .

Visually, the truth of the Archimedean Property seems clear. Why in the world would the Completeness Axiom be necessary to prove it?

Proof of the Archimedean Property in Baby Rudin

Before discussing this question, let’s work through the proof in Baby Rudin.

The proof is by contradiction and is fairly short. For your benefit, I will add more explanatory detail than is found in Rudin’s “polished” proof.

Proof of the Archimedean Property of the Real Numbers:

Suppose to the contrary that $nx\leq y\ \forall\ n\in \Bbb{N}$ . Let $A=\left\{nx\ |\ n\in \Bbb{N}\right\}$ . Then our assumption implies that $A$ is bounded above.

Here is where we use the completeness property of $\Bbb{R}$ . Since $A\subseteq \Bbb{R}$ and $\Bbb{R}$ is satisfies the least upper bound property, $\beta=\sup(A)$ exists in $\Bbb{R}.$

Since we are assuming that $x>0$ , we can say that $\beta-x<\beta$ so that $\beta-x$ is not an upper bound of $A$ (since $\beta$ is the least upper bound of $A$ ). But what does this mean? It means that $\exists\ m\in \Bbb{N}$ so that $mx\in A$ and $\beta-x<mx$ .

This last inequality is equivalent to $\beta<mx+x=(m+1)x$ . But $m\in \Bbb{N}\implies m+1\in \Bbb{N}$ . This, in turn, means that $(m+1)x\in A$ .

But this is a contradiction! The two conclusions we have just reached, that $\beta<(m+1)x$ and $(m+1)x\in A$ , imply that $\beta$ is not an upper bound of $A$ . But $\beta=\sup(A)$ , meaning $\beta$ is an upper bound of $A$ .

This logical contradiction means our original assumption that $nx\leq y\ \forall\ n\in \Bbb{N}$ must be false. Therefore, there exists an $n\in \Bbb{N}$ such that $nx>y$ .

Q.E.D.

The Ordered Field of Rational Numbers Satisfies the Archimedean Property

So the Completeness Axiom has clearly been used in the proof above. But again, why should that be necessary? After all, the ordered fields $\Bbb{Q}$ and $\Bbb{Q}(\sqrt{2})$ are not complete. But certainly the Archimedean Property holds true for them if for no other reason than they are subfields of $\Bbb{R}$ . Shouldn’t we be able to prove the Archimedean Property in some other way for these ordered fields?

Once again, it comes down to a matter of style (or “taste”). In other words, what we can prove depends on the approach we take. It depends on what our axioms and definitions are.

As done further above, we define $\Bbb{Q}$ to be a set of ratios of integers (or, more precisely, a collection of equivalence classes of such ratios) and define the less than symbol $<$ also as done above.

As a “new” axiom, we also assume that the set of natural numbers $\Bbb{N}$ is not bounded above. This could be proved as a theorem rather than stated as an axiom if we took the time to approach this using axiomatic set theory (e.g., Zermelo-Fraenkel set theory). But we will not do this.

Now we can state and prove the Archimedean Property of the rational numbers without reference to the real numbers.

Archimedean Property of $\Bbb{Q}$ : If $x,y\in \Bbb{Q}$ and $x>0$ , then there exists a positive integer $n\in \Bbb{N}$ such that $nx>y$ .

Proof of the Archimedean Property of the Rational Numbers:

If $y\leq 0$ , take $n=1$ . Now suppose $y>0$ . Then we can write $x=\frac{a}{b}$ and $y=\frac{c}{d}$ with $a,b,c,d\in \Bbb{N}$ .

By our assumption that $\Bbb{N}$ is not bounded above, we can choose $n\in \Bbb{N}$ such that $n>\frac{bc}{ad}$ . Then $nx>\frac{bc}{ad}\cdot \frac{a}{b}=\frac{c}{d}=y$ .

Q.E.D.

As an exercise, you might try to see if you can prove, without reference to the real numbers, that $\Bbb{Q}(\sqrt{2})$ satisfies the Archimedean Property. You may use the fact that $\Bbb{Q}$ does.

One lesson here is that, whichever way mathematical facts are proved, we need to start with assumptions — that is, axioms. Again, this might seem like “cheating”, but it is the only way we can get started.

Non-Archimedean Ordered Fields

Before looking at consequences of the Archimedean Property (many of which are equivalent to it), let us consider whether there are any ordered fields that do not satisfy the Archimedean Property. To be a bit more precise, we might wonder if there are one or more ordered field extensions of $\Bbb{Q}$ in which the Archimedean Property is not satisfied. That is, they are non-Archimedean ordered fields.

We might also wonder whether such field extensions of $\Bbb{Q}$ would necessarily have to be field extensions of $\Bbb{R}$ as well (certainly they could not be subfields of $\Bbb{R}$ ).

Let’s cut to the chase. Here are the answers. Yes, there are (infinitely) many field extensions of $\Bbb{Q}$ which are non-Archimedean. And no, they do not have to be field extensions of $\Bbb{R}$ (though there are such examples).

Fields of Rational Functions

To consider these examples, we start with a general construction.

Ring of Polynomials with Coefficients from a Field

Let $F$ represent an arbitrary field. In this context, the symbol $F[x]$ represents the so-called ring of polynomials with coefficients in $x$ . For example, if $F=\Bbb{R}$ , then $x^{3}+\pi x^{2}-\sqrt{3}x+\sqrt[3]{5}\in F[x]=\Bbb{R}[x]$ , but $(4+3i)x+2\not\in F[x]=\Bbb{R}[x]$ (where $i^{2}=-1$ ).

Such polynomials can be added and multiplied in the usual way. In addition, when the coefficients come from a field, there is no way that the product of two nonzero polynomials can be the zero polynomial. The ring $F[x]$ is also said to be an integral domain in this case.

Note however, that $F[x]$ is not a field. In fact, any non-constant polynomial (such as $x\in F[x]$ ) will not have a multiplicative inverse in $F[x]$ (note that $\frac{1}{x}\not\in F[x]$ since $\frac{1}{x}$ is not a polynomial).

The Field F Can Be Embedded in the Ring F[x] in a Natural Way

Note also (and this is very important) that any constant polynomial (with one “term” and no “variables”) in $F[x]$ can be considered to be an element of $F$ , even though we are initially thinking of it as a polynomial.

More precisely, there is a “natural” mapping $\varphi:F\longrightarrow F[x]$ that maps the element $c\in F$ to the constant polynomial $\varphi(c)=c\in F[x]$ . This mapping is an isomorphism of $F$ onto its image $\varphi(F)=\left\{\varphi(c)\ |\ c\in F\right\}$ that “embeds” $F$ in the “larger” set $F[x]$ .

Thus, we can effectively “pretend” that $F\subseteq F[x]$ , and even $F\subsetneq F[x]$ (or, if you prefer, $F\subset F[x]$ ), even though the “reality” is that $\varphi(F)\subsetneq F[x]$ instead.

If F is an Ordered Field, then F[x] is an Ordered Ring

In fact, if $F$ is an ordered field, then $F[x]$ is an ordered ring. Define a polynomial $f(x)\in F[x]$ to be positive (written $f>0$ ) if and only if its leading coefficient (coefficient of the highest power) is positive in $F$ . Note that this does not mean the “outputs” of $f(x)$ , when values from $F$ are substituted for $x$ , will be positive in $F$ .

Then, if $f(x),g(x)\in F[x]$ , define $f$ to be greater than $g$ (written $f>g$ ) if and only if $f-g>0$ . This definition of order is then consistent with the order defined on $F$ .

For example, in $F[x]=\Bbb{Q}[x]$ , if $f(x)=x^{2}$ and $g(x)=2x$ , then $f>0$ , $g>0$ , and $f>g$ since $f(x)-g(x)=x^{2}-2x$ has a positive leading coefficient. On the other hand, if $g(x)=2x^{2}$ , then $f<g$ since $f(x)-g(x)=-x^{2}$ .

Constructing a Field of Rational Functions

Let $F$ be an ordered field. Given any two nonzero polynomials $f(x),g(x)\in F[x]$ where $g(x)$ is nonzero, we can form the ratio $\frac{f(x)}{g(x)}$ . It turns out we may assume, without loss of generality, that this fraction has been reduced to lowest terms (by cancelling any common factors) and that the leading coefficient of $g(x)$ is positive (if it is not, multiply the top and bottom by $-1$ ).

Such a ratio of polynomials is often called a rational function, though our emphasis is on its algebraic character, rather than its graph or some other concept related to functions.

In fact, the set of all such rational functions can be made into an ordered field. This ordered field is denoted by $F(x)$ when the coefficients are elements of the ordered field $F$ (do not confuse $F(x)$ with function notation). And, as with the ring of polynomials $F[x]$ , there is a natural embedding (which is an ordered field isomorphism) of $F$ into $F(x)$ (as well as $F[x]$ in $F(x)$ ). This embedding maps the element $c\in F$ to the rational function $\frac{c}{1}\in F(x)$ .

In the end, we may “pretend” that $F\subsetneq F[x]\subsetneq F(x)$ . (This “pretending” is something mathematicians take seriously — it’s not a joke.)

What we have just done here is describe a special case of a more general construction: the field of fractions constructed from an arbitrary integral domain.

Defining the Order on 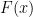$F(x)$

How is the order defined on $F(x)$ ? We can $\frac{f}{g}$ to be positive in $F(x)$ if and only if the leading coefficient of the polynomial $f(x)$ is positive (recall that we are assuming the leading coefficient of $g(x)$ is positive). Then we can say $\frac{f}{g}<\frac{j}{k}$ if and only if $\frac{j}{k}-\frac{f}{g}>0$ , where the subtraction is done by obtaining a common denominator, simplifying, and making sure the end result is in the standard form we assumed at the start.

The Ordered Field 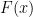$F(x)$ is Non-Archimedean

We claim the ordered field $F(x)$ does not satisfy the Archimedean Property; and we say that it is non-Archimedean.

To show this, we prove that no positive integer multiple of $\frac{1}{x}$ will ever be larger than the constant rational function $1=\frac{1}{1}$ . This is easy to verify with a brief calculation using the definitions above: $1-n\cdot \frac{1}{x}=\frac{x-n}{x}>0$ for any $n\in \Bbb{N}$ . Therefore, $n\cdot \frac{1}{x}<1$ for all $n\in \Bbb{N}$ . That does it! That proves $F(x)$ is non-Archimedean.

Because of this, we sometimes say that $\frac{1}{x}$ is “infinitesimal” compared to $1$ (see https://en.wikipedia.org/wiki/Archimedean_property#Non-Archimedean_ordered_field).

Along with a related example in Study Help for Baby Rudin, Part 1.2, “Definitions of Ordered Set and Ordered Field”, much of this content can also be found in the book “Counterexamples in Analysis”, by Gelbaum and Olmsted.

Alternative (Equivalent) Versions of the Archimedean Property

The following theorem represents the Archimedean Property of $\Bbb{R}$ in four different, but equivalent, forms.

Theorem: The following are equivalent (TFAE) and they are also all true.

If $x,y\in \Bbb{R}$ and $x>0$ , then there exists a positive integer $n\in \Bbb{N}$ such that $nx>y$ .
The set of positive integers (natural numbers) $\Bbb{N}$ is not bounded above.
For each $x\in \Bbb{R}$ , there exists an $n\in \Bbb{Z}$ such that $n\leq x<n+1$ . And there also exists an $m\in \Bbb{Z}$ such that $m<x\leq m+1$ . (When $x\not\in \Bbb{Z}$ , then $m=n$ . And when $x\in \Bbb{Z}$ , then $n=m+1$ .)
For each $x\in \Bbb{R}$ with $x>0$ , there exists $n\in \Bbb{N}$ such that $0<\frac{1}{n}<x$ (see the beginning of this article).

The proof of the equivalence of these statements is a good exercise. You should make sure you do it! To do so, prove that (1) implies (2), that (2) implies (3), that (3) implies (4), and that (4) implies (1).

I discuss these properties, without proof, in the following lecture.

Introduction to Real Analysis, Lecture 5: Crazy Functions, Archimedean Property of R, Cantor’s Theorem, Sequences

A Consequence of the Archimedean Property: Density of $\Bbb{Q}$ in $\Bbb{R}$

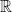
It is probably correct to say (without proof — LOL!) that the Archimedean Property has infinitely many applications. One of the most immediate one that is also fairly significant in real analysis implies that the set of rational numbers is “dense” in the set of real numbers. Between any two distinct real numbers can be found at least one rational number. (In fact, infinitely many rational numbers.) This is part (b) of Theorem 1.20 on page 9 of the third edition of Baby Rudin.

Theorem (Density of the Rationals in the Reals): If $x,y\in \Bbb{R}$ , then $\exists\ p\in \Bbb{Q}$ such that $x<p<y.$

The proof of this is a bit tricky and is a worthy exercise for you. It can also be found in Baby Rudin if you have trouble. I’ll give you the hint that you’ll need to apply the Archimedean Property more than once to prove it.

It also turns out that the set of irrational numbers $\Bbb{R}-\Bbb{Q}$ is dense in $\Bbb{R}$ as well. Between any two distinct real numbers there exists at least one irrational numbers. (In fact, infinitely many irrational numbers.)

However, even though both $\Bbb{Q}$ and $\Bbb{R}-\Bbb{Q}$ are both infinite sets which are both dense in $\Bbb{R}$ , it turns out, amazingly, that $\Bbb{R}-\Bbb{Q}$ is “bigger than” $\Bbb{Q}$ .

What does “bigger than” mean when referring to the relative “size” of two infinite sets? It can mean a few different things. Of most interest to us in the early stages of studying real analysis is the concept of “bigness” inherent in the concept of the so-called cardinality of a set. Much later, we will also look at this idea of relative size in terms of the so-called measure of a set.