Points, Coordinates, Skew Coordinates, and Graphs

Visual Linear Algebra Online, Chapter 1: Vectors, Matrices, and Linear Transformations (The First Chapter of an Online Textbook)

Section 1.1 (Referring to this Blog Post Titled “Points, Coordinates, Skew Coordinates, and Graphs” Above)

Determining the coordinates of two points in (slanted) skew coordinates.

What is the point? Wait a minute — that’s not the question I meant to ask here. I meant: What is a point?

How would you define a “point”? Maybe you would say “A point is…”

a dot, like a period.
something really, really, really, small (at the “opposite extreme” from infinity) — like an atom or maybe even an electron.
a location.
a geometric object that has no length, area, or volume.

Are any of these descriptions satisfactory? Not really, though if I had to choose, I would say options 3 and 4 are “best”. On the other hand, we certainly typically draw points as if they are “dots like a period” from option 1. Option 2 might be thought of as an approximate physical representation of a point. And, in fact, physicists often speak of “point particles”. But Option 2 does not fully capture how “truly small” a point is.

Visualizing a Point

Option 4 takes precedence over option 1 because you should realize that zooming in on a point should not change how big you make it look when you draw it. That is, points should look the same at all levels of magnification. They do NOT “get bigger” as you zoom in closer.

Points should be visualized in a way that emphasizes that the are zero-dimensional. — Points are typically drawn to look the same at every scale (every level of magnification), though how big you draw it is up to you. The picture on the right is **NOT** the correct way to visualize zooming in on a point.

The best approach is actually to leave the notion of a point as intuitive, but undefined. This helps us to avoid circularity in our definitions. It actually helps us to avoid confusion as well. This is one important example of a mathematical abstraction.

So far, we are implicitly assuming that points must lie in a plane. This is partially because this is the most typical way of visualizing them. We will continue making this assumption for most of Section 1.1 of Visual Linear Algebra Online (this blog post). But you should realize that points can be in be in “spaces” of any dimension — even spaces with more than three dimensions! In fact, even spaces with infinitely many dimensions! Hey, Infinity is Really Big!

Video for Section 1.1 of Visual Linear Algebra Online

Here is a video I made that includes a summary of the content of this first section of Visual Linear Algebra Online. The written text for Section 1.1 continues further below.

Visual Linear Algebra Online at Infinity is Really Big (the First Section of an Online Textbook)

Rectangular Coordinates in “the” Plane

The play on words at the very beginning of Section 1.1 is a bit of a punny joke. Since there are (infinitely) many different points that can be considered, it does not make sense to speak of “the” point.

However, you will sometimes hear mathematicians speak of “the” line or “the” plane. This is in spite of the fact that there are infinitely many different lines and planes that can be considered. Don’t worry about this too much. Essentially, when we speak of “the” line or “the” plane, we just want to draw our attention to the fact that we are focused on either a one-dimensional or a two-dimensional situation.

It is important to realize that we imagine both “the” line and “the” plane have infinite extent. The line goes on forever in both (one-dimensional) directions and the plane goes on forever in all (two-dimensional) directions.

The Ancient Greeks, the Arabs, and the 17th Century Frenchmen

The ancient Greek mathematicians (such as Pythagoras, Eudoxus, Euclid, and Archimedes) were interested in geometric objects in their “pure” form. They worked with things like points, lines, triangles, circles, cylinders, spheres almost as if they were actual physical objects (though many like Plato viewed them as idealized “forms”). While they did consider descriptive magnitudes such as lengths, areas, volumes, and angle measures, there was little movement toward understanding these objects, magnitudes, and their relationships in terms of variables or a fixed frame of reference.

The notion of a reference frame had to wait many years until after the development of symbolic algebra in the Levant and the Arabian Peninsula. Then, in the 1600’s, Frenchmen René Descartes and Pierre de Fermat used this symbolic algebra and their imaginations to define the idea of rectangular coordinates in the plane. This system of coordinates is often called Cartesian coordinates in honor of the former of these two intellectuals.

One of the main points of emphasis in this section of Visual Linear Algebra Online is that these ideas can be generalized to, for example, skew coordinates and polar coordinates. We will ultimately see that skew coordinates, in particular, are very important in linear algebra and its applications.

Construction of Rectangular Axes and Gridlines

How is the rectangular coordinate system defined? Start by defining a unit of length. Physically-speaking, you could use something like a centimeter in this definition. Then “impose” a set of two axes (directed lines) on the plane that are perpendicular to each other. The point at the intersection of the two axes is called the origin and is sometimes labeled $\mathcal{O}$ .

Next, mark off points on these two lines that are each one unit apart and label them as shown in the picture below. Also, label the two axes. The traditional labels are “x” and “y“. This labeling is part of how the symbolic algebra starts to come into play. These letters will represent (real-valued) “variables”. But, at the moment, they are just names for the axes.

Rectangular coordinates are imposed on the plane. The point of intersection of the two axes is called the origin. — *Imposition of a set of rectangular axes (perpendicular to each other) on the plane. The point of intersection is called the origin and labeled $\mathcal{O}.$*

*Imposition of a set of rectangular axes (perpendicular to each other) on the plane. The point of intersection is called the origin and labeled $\mathcal{O}.$*

Once this has been done, use these axes to define a rectangular grid. In essence, it is as if you are making graph paper as shown below.

Rectangular Coordinates

Each point in the plane now has a unique “address”: its rectangular coordinates. For any given point $P$ , draw a vertical and a horizontal line through $P$ . The location where the vertical line intersects the horizontal $x$ -axis is called the first coordinate of $P$ . The location where the horizontal line intersects the vertical $y$ -axis is called the second coordinate of $P$ .

There are three points $P, Q$ , and $R$ in the picture below, along with the corresponding vertical and horizontal lines described in the paragraph above.

Rectangular coordinates are determined by where vertical and horizontal lines through a given point intersect the axes. — The three points $P,Q$ , and $R$ have rectangular coordinates $(4.2,-2.8), (6.8,4.5)$ , and $(-6.4,8)$ , respectively.

The three points $P,Q$ , and $R$ have rectangular coordinates $(4.2,-2.8), (6.8,4.5)$ , and $(-6.4,8)$ , respectively.

Since the vertical (red) line through $P$ intersects the horizontal $x$ -axis at about $4.2,$ we say that this is the first coordinate of $P$ . Since the horizontal (red) line through $P$ intersects the vertical $y$ -axis at about $-2.8,$ we say that this is the second coordinate of $P$ . The rectangular coordinates of $P$ then are written as an “ordered pair” $(x,y)=(4.2,-2.8)$ . With this labeling, the first coordinate is also called the $x$ -coordinate and the second coordinate is also called the $y$ -coordinate.

Likewise, the rectangular coordinates of $Q$ are $(x,y)=(6.8,4.5)$ and the rectangular coordinates of $R$ are $(x,y)=(-6.4,4.8)$ .

Signed Distance Interpretation

In addition to the interpretation we have just given, the rectangular coordinates can be thought of as signed distances to the axes. In particular, since the rectangular coordinates of $P$ are $(x,y)=(4.2,-2.8),$ we can say that $P$ is $4.2$ units to the right of the vertical $y$ -axis and is $2.8$ units below the horizontal $x$ -axis.

For ease of reference and visualization, we will commonly abuse notation and write $P=(x,y)=(4.2,-2.8)$ , even though $P$ is a point and not an ordered pair. The following animation of a moving point emphasizes the signed distance interpretation of the coordinates as well as the notation just mentioned — there is also a connection to trigonometry!

Rectangular coordinates can be thought of as signed distances from the axes. — The (first) $x$ -coordinate of $P$ (in blue) is the signed horizontal distance to the vertical $y$ -axis. It is positive when the point is to the right of the $y$ -axis and negative when the point is to the left. The (second) $y$ -coordinate of $P$ (in brown) is the signed vertical distance to the horizontal $x$ -axis. It is positive when the point is above the $y$ -axis and negative when the point is below.

The (first) $x$ -coordinate of $P$ (in blue) is the signed horizontal distance to the vertical $y$ -axis. It is positive when the point is to the right of the $y$ -axis and negative when the point is to the left. The (second) $y$ -coordinate of $P$ (in brown) is the signed vertical distance to the horizontal $x$ -axis. It is positive when the point is above the $y$ -axis and negative when the point is below.

A final comment for this section: a coordinate plane is often described using the labels for the axes. If the axes are labeled with $x$ and $y$ , the coordinate plane is called the $xy$ -plane.

Equations and Graphs: Big Benefits of Coordinates

Once rectangular coordinates have been defined on the plane, we are set to make use of the foundational correspondence between equations and graphs. It is difficult to overstate how historically important this correspondence has been — both for mathematics and its applications. The book Infinite Powers: How Calculus Reveals the Secrets of the Universe, by Steven Strogatz is a very clear, thorough, and interesting account of why this correspondence has been so important. The study of the correspondence between equations and graphs is so vast and profound that it is essentially a field of study: called analytic geometry.

How does this correspondence work? For “nice” equations and “nice” graphs, it is two-way. Given any “nice” equation, it has a “nice” graph. Conversely, given any “nice” graph, it can at least be approximated by a “nice” equation. We leave the word “nice” undefined, except to say that it includes most of the examples you have probably considered in your past mathematics courses.

On the other hand, the word “nice” definitely applies to equations that are linear.

Linear Equations, Nonlinear Equations, and Graphs

In algebra and precalculus classes, a linear equation in two variables $x$ and $y$ is defined to be one that can be put in the form $ax+by=c$ for some constants $a,b,$ and $c$ . It is assumed that either $a\not=0$ or $b\not=0$ (most typically, both $a\not=0$ and $b\not=0$ ). Note that the variables $x$ and $y$ are both raised to the first power.

A nonlinear equation is one that cannot be put in this form. This typically means that the equation has other powers of $x$ and/or $y$ , or that there are expressions involving “transcendental functions” such as $\sin(x)$ or $e^{x}$ in the equation.

Given any equation involving two variables $x$ and $y$ , its graph is defined as follows. It is the set of points $P$ in the rectangular $xy$ -plane whose coordinates $(x,y)$ make the equation true. In other words, when you substitute each such pair of numbers in the equation simultaneously, you get a true statement.

In a rectangular coordinate system, linear equations have graphs which are straight lines and nonlinear equations have graphs which are not straight lines.

Example 1: Draw the graph of the (linear) equation $4x+5y=10$

You could start solving this problem by guessing some points on the graph. For example, the points whose coordinates are $(x,y)=(0,2)$ and $(x,y)=(2.5,0)$ both satisfy the equation (make it true). This is because $4\cdot 0+5\cdot 2=10$ and $4\cdot 2.5+5\cdot 0=10$ . Another point that can be guessed is the one whose coordinates are $(x,y)=(1.25,1)$ , since $4\cdot 1.25+5\cdot 1=5+5=10$ .

A more systematic approach is to solve for $y$ as a function of $x$ . Then pick various values of $x$ and use the function to find the corresponding values of $y$ .

Here are the algebra steps: $4x+5y=10\Rightarrow 5y=10-4x\Rightarrow y=2-\frac{4}{5}x$ . The expression on the right-hand side of the last equation defines a function $f$ by the formula $f(x)=2-\frac{4}{5}x$ . The graph of this function is the same as the graph of the original equation.

Now we can make a table of values using a variety of choices for the “independent variable” $x$ . For example, if we choose $x=2$ , then $y=f(2)=2-\frac{4}{5}\cdot 2=\frac{10}{5}-\frac{8}{5}=\frac{2}{5}=0.4$ .

Here is an example table of values:

$\begin{array}{|c||c|c|c|c|c|c|c|}\hline x & -3 & -2 & -1 & 0 & 1 & 2 & 3 \\ \hline y=f(x) & 4.4 & 3.6 & 2.8 & 2 & 1.2 & 0.4 & -0.4 \\ \hline \end{array}$

Here is the corresponding plot with the points from the table highlighted. The graph can be seen to be a straight line by plotting even more points.

The graph of a linear equation in a rectangular (Cartesian) coordinate system is a straight line. — The graph of the linear equation $4x+5y=10$ is a straight line in rectangular coordinates. This graph is the same as the graph of the function $y=f(x)=2-\frac{4}{5}x$ . It is a line of slope $-\frac{4}{5}$ and vertical axis intercept at $y=2$ .

The graph of the linear equation $4x+5y=10$ is a straight line in rectangular coordinates. This graph is the same as the graph of the function $y=f(x)=2-\frac{4}{5}x$ . It is a line of slope $-\frac{4}{5}$ and vertical axis intercept at $y=2$ .

Example 2: Draw the graph of the (nonlinear) equation $x^{2}+y=3$

By inspection, we quickly see that the points with rectangular coordinates $(1,2), (-1,2),$ and $(0,3)$ are on the graph. To be more systematic, we solve for $y$ to get $y=f(x)=-x^{2}+3$ and then make a table of values. One such table is:

$\begin{array}{|c||c|c|c|c|c|c|c|}\hline x & -3 & -2 & -1 & 0 & 1 & 2 & 3 \\ \hline y=f(x) & -6 & -1 & 2 & 3 & 2 & -1 & -6 \\ \hline \end{array}$

Plotting even more points produces the graph below. It is not a straight line. It turns out to be a special curve called a parabola, however.

The graph of a nonlinear function in a rectangular (Cartesian) coordinate system is not a straight line. — *The graph of the nonlinear equation $x^{2}+y=3$ is not a straight line in rectangular coordinates. This graph is the same as the graph of the function $y=f(x)=-x^{2}+3$ . It is a parabola.*

*The graph of the nonlinear equation $x^{2}+y=3$ is not a straight line in rectangular coordinates. This graph is the same as the graph of the function $y=f(x)=-x^{2}+3$ . It is a parabola.*

Skew Coordinates (a.k.a. Skew Coordinate Systems)

Is there anything special about rectangular (Cartesian) coordinates?

Yes. What makes the system of rectangular coordinates special is that it is relatively easy to understand and to use. It seems natural to draw a grid with horizontal and vertical lines like this.

But must we use rectangular coordinates? For example, do the coordinate axes have to be perpendicular to each other?

The answer is “no”. We could use, if we want, a system of slanted coordinates, which are more officially called skew coordinates. In such a system, the coordinate axes are not perpendicular to each other.

Of course, you could ask why we would do such a thing. At the moment, it will suffice to say that doing so makes many problems easier to think about and to solve. You could even say it is a big part of the purpose of the entire subject of linear algebra. We will see many examples of this in later chapters, where we consider the idea of a change of basis.

Example of Skew Coordinates

An example of a skew coordinate system we can consider is one where the vertical axis stays vertical, but the horizontal axis becomes slanted. Maybe we make the non-vertical axis to be slanted at a $45^{\circ}$ angle from its original position. Below is a picture of this situation. The origin $\mathcal{O}$ is still the spot where the axes intersect. The axes have been relabeled with $u$ and $v$ . This is in spite of the fact that the vertical axis has not changed.

Slanted axes for a system of skew coordinates (a skew coordinate system). — A slanted coordinate system imposed on the plane. The origin is still labeled with $\mathcal{O}$ . The ‘new’ axes have been labeled $u$ and $v$ . The tick marks shown are still one unit of distance apart.

But if we do this, how should the “address” of any given point be determined? The most natural way is to make use of a slanted grid like the one shown below. This is like having slanted graph paper. Each of these lines corresponds to either the value of $u$ or the value of $v$ being constant.

An example of skew coordinates. The horizontal axis has become slanted at a 45 degree angle. — *Slanted gridlines generated from slanted axes. Each of these lines corresponds to either the value of $u$ or the value of $v$ being constant.* This is an example of skew coordinates.

*Slanted gridlines generated from slanted axes. Each of these lines corresponds to either the value of $u$ or the value of $v$ being constant.* This is an example of skew coordinates.

Estimating New Skew Coordinates by Eye

Now consider the points $P$ and $Q$ in the slanted skew coordinate system below. In the original (old) $xy$ -coordinate plane, the coordinates of $P$ were $(2,0)$ and the original coordinates of $Q$ were $(-4,-1)$ . The red and blue lines shown indicate how to find their “new” coordinates in the “new” $uv$ -plane. Can you guess their approximate new coordinates before reading on?

*In the original rectangular coordinates, $P=(x,y)=(2,0)$ and $Q=(x,y)=(-4,-1)$ . Can you guess their approximate “new” $(u,v)$ -coordinates?*

*In the original rectangular coordinates, $P=(x,y)=(2,0)$ and $Q=(x,y)=(-4,-1)$ . Can you guess their approximate “new” $(u,v)$ -coordinates?*

By my rough eyeball estimate, I guess that the new skew coordinates of $P$ are $(u,v)\approx (2.8,-2)$ . I also guess that the new skew coordinates of $Q$ are $(u,v)\approx (-5.7,3)$ . Make sure you understand why!

For $P$ , the reason is that the slanted dashed red line is about 2.8 units long (in the positive direction from the vertical $v$ -axis) and the vertical dashed red line is about 2 units long (in the negative direction from the slanted $u$ -axis). For $Q$ , the slanted dashed blue line is about 5.7 units long (in the negative direction from the vertical $v$ -axis) and the vertical dashed blue line is about 3 units long (in the positive direction from the slanted $u$ -axis).

Transforming One System to the Other and Vice Versa

There is actually a system of (linear) equations that will “transform” the old (rectangular) coordinates $(x,y)$ into the new (slanted) skew coordinates $(u,v)$ . For this example, this system happens to be:

$\begin{array}{rcl} u & = & \sqrt{2}x \\ v & = & -x+y \end{array}$

For example, take the point $Q$ from above. Its rectangular coordinates were $(x,y)=(-4,-1)$ . Plugging these values into this system of equations gives $u=-4\sqrt{2}\approx -5.7$ and $v=-(-4)+(-1)=3$ so that $(u,v)\approx (-5.7,3)$ , just as was guessed above.

Moreover, this system can be solved for $x$ and $y$ to obtain a new system of linear equations that will go back the other direction (like an inverse function). It will “transform” the new (slanted) skew coordinates $(u,v)$ into the old (rectangular) coordinates. For this example, this system happens to be:

$\begin{array}{rcl} x & = & \frac{1}{\sqrt{2}}u \\ y & = & \frac{1}{\sqrt{2}}u+v \end{array}$

Note that if $u=-4\sqrt{2}$ and $v=3$ , then these equations give $x=\frac{1}{\sqrt{2}}\cdot (-4\sqrt{2})=-4$ and $y=\frac{1}{\sqrt{2}}\cdot (-4\sqrt{2})+3=-4+3=-1$ so that $(x,y)=(-4,-1)$ .

Graphs and Equations Can Get Transformed Too

Given an equation in the original $xy$ -coordinates, we can see what happens if we graph the same equation in the new $uv$ -coordinates. In addition, given a graph with a certain equation in the original $xy$ -coordinates, we can see if we can find new $uv$ -coordinate equation for that same graph.

If that is confusing to you, a couple examples should help.

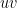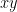Example 3: Draw the graph of the (linear) equation $4u+5v=10$ in the slanted $uv$ -plane. Also, represent the straight line graph of $4x+5y=10$ from the original $xy$ -plane in terms of the new 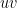$uv$ -coordinates.

To graph $4u+5v=10$ in the slanted $uv$ -plane, we can use the same procedure as in Example 1. However, we must use the (slanted) skew coordinates to make our graph. We solve for $v$ as a function of $u$ to get $v=f(u)=2-\frac{4}{5}u$ . This gives the same table of values as before (but relabeled).

$\begin{array}{|c||c|c|c|c|c|c|c|}\hline u & -3 & -2 & -1 & 0 & 1 & 2 & 3 \\ \hline v=f(u) & 4.4 & 3.6 & 2.8 & 2 & 1.2 & 0.4 & -0.4 \\ \hline \end{array}$

Here is what the new graph looks like in the skew coordinate system, along with the seven points from the table above. Make sure you understand how these points are plotted using the values of $u$ and $v$ , as well as the slanted gridlines. Also note that the graph of this linear equation is still a straight line, even though the coordinate system is skewed.

The graph of a linear function in skew coordinates is a straight line. — The graph of $4u+5v=10$ in the skew $uv$ -coordinate system. Note, for example, that the black point on the far right has new coordinates $(u,v)=(3,-0.4)$ . Also note that the graph is still a straight line, even in skew coordinates.

The graph of $4u+5v=10$ in the skew $uv$ -coordinate system. Note, for example, that the black point on the far right has new coordinates $(u,v)=(3,-0.4)$ . Also note that the graph is still a straight line, even in skew coordinates.

To represent the original line $4x+5y=10$ from Example 1 in the new coordinates, just use the transformation equations from above: $x= \frac{1}{\sqrt{2}}u$ and $y=\frac{1}{\sqrt{2}}u+v$ . Substituting these converts $4x+5y=10$ to $4\cdot \frac{1}{\sqrt{2}}u+5\cdot \left(\frac{1}{\sqrt{2}}u+v\right)=10$ . This simplifies to $\frac{9}{\sqrt{2}}u+5v=10$ . If you graph this equation in the slanted $uv$ -coordinates, you will get the same line (visually-speaking) as the one from Example 1.

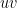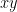Example 4: Draw the graph of the (nonlinear) equation $u^{2}+v=3$ in the slanted $uv$ -plane. Also, represent the parabolic graph of $x^{2}+y=3$ from the original $xy$ -plane in terms of the new 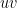$uv$ -coordinates.

In our final example we do the same kind of thing as in Example 3, except for the nonlinear situation from Example 2.

Solving $u^{2}+v=3$ for $v$ as a function of $u$ gives $v=f(u)=-u^{2}+3$ . The table of points to plot is the same as before, but relabeled.

$\begin{array}{|c||c|c|c|c|c|c|c|}\hline u & -3 & -2 & -1 & 0 & 1 & 2 & 3 \\ \hline v=f(u) & -6 & -1 & 2 & 3 & 2 & -1 & -6 \\ \hline \end{array}$

We must plot these points with respect to the new slanted coordinates. Doing so gives the following graph. Note that it still seems to be a parabola. This is indeed the case.

The graph of a quadratic function in skew coordinates is a parabola. — The graph of $u^{2}+v=3$ in the skew $uv$ -coordinate system. Note, for example, that the black point on the far right has new coordinates $(u,v)=(3,-6)$ . Also note that the graph is still a parabola, even in skew coordinates.

The graph of $u^{2}+v=3$ in the skew $uv$ -coordinate system. Note, for example, that the black point on the far right has new coordinates $(u,v)=(3,-6)$ . Also note that the graph is still a parabola, even in skew coordinates.

Another interesting aspect of this particular graph is that there is a 3D (three-dimensional) kind of effect if you look at it in the right way. It’s almost as if you are looking at the ordinary rectangular coordinate system, but with perspective. From this 3D perspective, the positive $u$ -axis should seem like it is closer to you than the negative $u$ -axis is. Also, the parabola would actually be the same as the one in the rectangular coordinate system when you imagine this picture with perspective.

To represent the original parabola $x^{2}+y=3$ from Example 2 in the new coordinates, just use the transformation equations from above: $x= \frac{1}{\sqrt{2}}u$ and $y=\frac{1}{\sqrt{2}}u+v$ . Substituting these converts $x^{2}+y=3$ to $\left(\frac{1}{\sqrt{2}}u\right)^{2}+\frac{1}{\sqrt{2}}u+v=3$ . This simplifies to $\frac{1}{2}u^{2}+\frac{1}{\sqrt{2}}u+v=3$ . If you graph this equation in the (slanted) skew $uv$ -coordinates, you will get the same parabola (visually) as the one from Example 2.

Nonlinear Coordinates

There are also plenty of nonlinear coordinate systems. For the plane, the most common and useful of these is polar coordinates. For polar coordinates, there are no “axes” in the same sense as before (though we usually draw the ordinary rectangular axes for reference).

Instead, we start by picking the origin $\mathcal{O}$ of the plane and drawing a horizontal ray emanating from it. Draw tick marks one unit apart on this ray and then draw circles centered at the origin whose radii are the distances from the origin to these tick marks. Finally, draw other rays emanating from the origin at various angles from the original ray. The result is a polar coordinate system with a polar grid as shown below.

A polar grid for polar coordinates. — Polar grid for polar coordinates. The rectangular $x$ and $y$ axes are in the picture for the sake of reference. The original ’emanating ray’ from the origin is the positive $x$ -axis. The angles are all $15^{\circ}$ apart, which is the same as $\frac{\pi}{12}\approx 0.262$ radians.

Polar grid for polar coordinates. The rectangular $x$ and $y$ axes are in the picture for the sake of reference. The original ’emanating ray’ from the origin is the positive $x$ -axis. The angles are all $15^{\circ}$ apart, which is the same as $\frac{\pi}{12}\approx 0.262$ radians.

The polar coordinates of any point $P$ are written as $(r,\theta)$ . The symbol $r$ represents the distance of the point to the origin. The symbol $\theta$ represents an angle that the ray $\overrightarrow{\mathcal{O}P}$ makes with the positive $x$ -axis. The value of $\theta$ is not unique. In fact, the value of $r$ is not unique either if we allow $r$ to represent a signed distance. In this case, a negative signed distance is taken to occur along the “opposite ray” from the ray $\overrightarrow{\mathcal{O}P}$ with angle $\theta$ .

Graphing a Function in Polar Coordinates

An interesting thing here is that a “linear” function, such as $r=f(\theta)=2-\frac{4}{5}\theta$ , will actually have a graph in polar coordinates that is not a straight line. Here’s the relevant table of data in polar coordinates:

$\begin{array}{|c||c|c|c|c|c|c|c|}\hline \theta & -3 & -2 & -1 & 0 & 1 & 2 & 3 \\ \hline r=f(\theta) & 4.4 & 3.6 & 2.8 & 2 & 1.2 & 0.4 & -0.4 \\ \hline \end{array}$

You should make sure you understand that $\theta$ is measured in radians here. One complete revolution around the origin corresponds to $2\pi\approx 6.28$ radians.

Below is the graph of this function with the same special points plotted as in Examples 1 and 3, but now in polar coordinates. It’s no line, but isn’t it beautiful?

The graph of a linear function in polar coordinates is no longer a straight line. — In polar coordinates, the graph of the ‘linear’ function $r=f(\theta)=2-\frac{4}{5}\theta$ is no longer a straight line, but it sure is beautiful. Check that each of the black dots shown has polar coordinates from the table above. For the last one, $r$ must be interpreted as a signed distance (a distance along the ‘opposite ray’).

In polar coordinates, the graph of the ‘linear’ function $r=f(\theta)=2-\frac{4}{5}\theta$ is no longer a straight line, but it sure is beautiful. Check that each of the black dots shown has polar coordinates from the table above. For the last one, $r$ must be interpreted as a signed distance (a distance along the ‘opposite ray’).

A nonlinear transformation that takes polar coordinates $(r,\theta)$ and converts them back to rectangular coordinates $(x,y)$ can be found using trigonometry. The transformation is:

$\begin{array}{rcl} x & = & r\cos(\theta) \\ y & = & r\sin(\theta) \end{array}$

Converting from $(x,y)$ to $(r,\theta)$ takes more care and involves the arctangent (inverse tangent) function $\arctan(x)=\tan^{-1}(x)$ . We leave this for the exercises.

Exercises about Rectangular Coordinates

For the linear equation $2x-3y=4$ , (a) Solve for $y$ as a function of $x$ , (b) Make a table of values of this function for $x=-3,-2,-1,0,1,2,3$ , (c) Graph the resulting points and also the resulting the line in the rectangular $xy$ -plane.
For the nonlinear equation $x^{3}+y=-1$ , (a) Solve for $y$ as a function of $x$ , (b) Make a table of values of this function for $x=-3,-2,-1,0,1,2,3$ , (c) Graph the resulting points and also the resulting line in the rectangular $xy$ -plane.
Consider (rotated) skew coordinates where the $u$ -axis is at a $45^{\circ}$ angle from the $x$ -axis and the $v$ -axis is at a $45^{\circ}$ angle from the $y$ -axis, as shown below. (a) Graph the linear equation $2u-3v=4$ in this (rotated) skew coordinate system. Is the result a line? (b) Graph $u^{3}+v=-1$ in this (rotated) skew coordinate system. Does the result still resemble the graph of a cubic function in the variables $x$ and $y$ ?

A system of skew coordinates obtained by a 45 degree counterclockwise rotation of standard rectangular coordinates. — Rotated coordinate system for Exercise #3 (this could also be thought of as slanted).

Transformations Between Coordinates

4. For #3, the system of linear equations that transforms the “old” rectangular coordinates $(x,y)$ into the “new” (rotated) skew coordinates $(u,v)$ is:

$\begin{array}{rcl} u & = & \frac{1}{\sqrt{2}}x + \frac{1}{\sqrt{2}}y \\ v & = & -\frac{1}{\sqrt{2}}x+\frac{1}{\sqrt{2}}y \end{array}.$

On the other hand, the “inverse” system of linear equations that transforms the “new” (rotated) skew coordinates $(u,v)$ into the “old” rectangular coordinates $(x,y)$ is:

$\begin{array}{rcl} x & = & \frac{1}{\sqrt{2}}u - \frac{1}{\sqrt{2}}v \\ y & = & \frac{1}{\sqrt{2}}u+\frac{1}{\sqrt{2}}v \end{array}.$

(a) Use the first of these systems to find the “new” (rotated) skew coordinates $(u,v)$ of the point $P$ with “old” rectangular coordinates $(x,y)=(1,1)$ . (b) Use the second of these systems to take your answer from part (a) and convert it back to rectangular coordinates. (c) Use the first of these systems to convert $2u-3v=4$ to rectangular $(x,y)$ coordinates and simplify. Do you still get a linear equation? (d) Use the first of these systems to convert $u^{3}+v=-1$ to rectangular $(x,y)$ coordinates. Is it possible to solve the resulting equation for $y$ as a cubic function of $x$ in any kind of simple way?

Exercises about Polar Coordinates

5. (a) Find the exact rectangular $(x,y)$ coordinates of a point $P$ whose polar coordinates are $(r,\theta)=\left(4,\frac{\pi}{6}\right)$ (where $\theta$ is in radians). (b) Graph this point.

6. (a) Find the exact polar $(r,\theta)$ coordinates of a point $P$ whose rectangular coordinates are $(x,y)=(-3,3\sqrt{3})$ . (b) Graph this point.

7. Use polar coordinates to carefully graph the function $r=f(\theta)=\sqrt{\theta}$ , where $\theta$ is in radians and $0\leq \theta\leq 16$ .

8. Use polar coordinates to carefully graph the function $r=f(\theta)=\sin(3\theta)$ , where $\theta$ is in radians and $0\leq \theta\leq 2\pi$ .

Next: Section 1.2, Vectors in Two-Dimensions