The Inverse Matrix of a Linear Transformation

Visual Linear Algebra Online, Section 1.9

*The inverse of a rotation is another rotation by the same angle, but in the opposite direction.*

Inverse functions are a kind of high-technology in mathematics. They can help you solve infinitely many problems at once!

In linear algebra, some linear transformations on finite-dimensional Euclidean space ${\Bbb R}^{n}$ have inverse functions. Those that do have an associated inverse matrix. In this section, our main goals are to explore how to calculate the inverse matrix and to see how it is useful.

A Basic Example

But let’s start with a basic example of an inverse function.

Suppose the height above the ground, in meters, of a falling object, as a function of time, in seconds, is $h=f(t)=490-4.9t^{2}$ . The graph of this function is shown below. Note that the appropriate domain for this application consists of those values of $t\geq 0$ where $h\geq 0$ . This is equivalent to $0\leq t\leq 10$ seconds.

The height of a falling object as a function of time. (Free fall without air resistance) — The height above the ground, in meters, of an falling object as a function of time, in seconds, is $h=f(t)=490-4.9t^{2}$ .

This function is decreasing because the object is falling. The graph is also concave down because the object falls faster and faster over time.

How long will it take the object to reach a height of 100 meters? Just set $h=100$ and solve for $t$ .

$100=490-4.9t^{2}\Rightarrow 4.9t^{2}=390\Rightarrow t=\sqrt{\frac{390}{4.9}}\approx \sqrt{79.592}\approx 8.9\mbox{ seconds}$ .

Solving the General Problem

What if we want to solve this problem for an arbitrary height $h$ ? The same steps give us the inverse function $f^{-1}$ of $f$ . It will solve the general problem.

$h=490-4.9t^{2}\Rightarrow 4.9t^{2}=490-h\Rightarrow t=\sqrt{\frac{490-h}{4.9}}\approx \sqrt{100-0.204h}$ .

The inverse function $t=f^{-1}(h)=\sqrt{\frac{490-h}{4.9}}$ represents the solution to infinitely many problems: every problem where we solve $h=100-4.9t^{2}$ for $t$ . In other words, if we are given an arbitrary height above the ground $h$ , this function computes the amount of time $t$ it takes to fall to that height.

When the independent and dependent variables of a function have no real-life meaning, it is traditional to swap the variables when finding an inverse function. When this is done and the axes have the same scale, the graphs of the function and its inverse are reflections of each other across the $45^{\circ}$ diagonal line through the origin.

However, if the variables do have real-life meaning, the variables should not be swapped.

This is the case for our example. In this case, it is better to graph $t=f^{-1}(h)=\sqrt{\frac{490-h}{4.9}}$ by swapping the axes of the original graph instead, as shown below. The domain of this function for this application is the interval $\{h\in {\Bbb R}\, |\, 0\leq h\leq 490\}$ .

*The time, in seconds, of an falling object as a function of height above ground, in meters, to which it has fallen is $t=f^{-1}(h)=\sqrt{\frac{490-h}{4.9}}$ .*

This function is decreasing and concave down as well. This also reflects the fact that the object falls at a faster and faster rate over time, though explaining why this is true is more difficult.

Composition of the Function and Its Inverse

In Section 1.8, “Matrix Multiplication and Composite Transformations” we discussed function composition. This is where two functions are applied in sequence. It can also be thought of as “plugging one function into another”. A small circle $\circ$ is used to represent the binary operation of function composition, where two functions are combined in this way to obtain a third function.

There is an intimate relationship between a function and its inverse with respect to function composition. Let’s see what happens when we compose the functions for our example above.

For $f^{-1}\circ f$ , we get

$(f^{-1}\circ f)(t)=f^{-1}(f(t))=f^{-1}(490-4.9t^{2})=\sqrt{\frac{490-(490-4.9t^{2})}{4.9}}=\sqrt{t^{2}}=|t|$ .

However, since we are assuming that $t\geq 0$ , it follows that $|t|=t$ and therefore $(f^{-1}\circ f)(t)=t$ for all $t$ in the domain of $f$ .

Here is the computation for $f\circ f^{-1}$ .

$(f\circ f^{-1})(h)=f(f^{-1}(h))=f\left(\sqrt{\frac{490-h}{4.9}}\right)$ $=490-4.9\left(\sqrt{\frac{490-h}{4.9}}\right)^{2}=490-(490-h)=h$

This is true for all $h$ in the domain of $f^{-1}$ .

In both cases we see that $f$ and $f^{-1}$ “undo” each other. The output of the composite function is the same as the input.

It should also be clear that we need to be careful in discussing the domains of these functions. For example, if $t<0$ , then $|t|=-t$ instead. Also, if $h>490$ , then $\sqrt{\frac{490-h}{4.9}}$ is an imaginary number, which we would want to avoid for this application.

You may have also noted that if we consider the domain of $f(t)=490-4.9t^{2}$ to be all of ${\Bbb R}$ instead of the interval $[0,10]$ , then $f$ is no longer a one-to-one function. This would mean it has no inverse function. The domain must be restricted in order for an inverse function to exist.

Inverse Functions in General

Let $A$ and $B$ be two nonempty sets. Suppose $f$ is a function with domain $A$ and codomain $B$ . Notationally, we have represented this situation as $f:A\longrightarrow B$ or $A\xrightarrow{\ \ f\ \ }B$ .

One-to-One (Injective) and Onto (Surjective) Functions

In previous sections, such as Section 1.5 “Matrices and Linear Transformations in Low Dimensions”, we have already discussed what it means for a function to be one-to-one (injective) and/or onto (surjective). However, here we will state precise definitions.

Definition of One-to-One (Injective) and Examples

Definition 1.9.1: A function $f:A\longrightarrow B$ is one-to-one (injective) if distinct inputs give distinct outputs. That is, $f$ is one-to-one if $a_{1}\not=a_{2}$ implies that $f(a_{1})\not=f(a_{2})$ . This is equivalent to saying that $f(a_{1})=f(a_{2})$ implies that $a_{1}=a_{2}$ .

As a quick example, consider the function $f:{\Bbb R}\longrightarrow {\Bbb R}$ defined by $f(x)=4x-5$ . If $f(a_{1})=f(a_{2})$ , then $4a_{1}-5=4a_{2}-5$ . Adding 5 to both sides of this equation gives $4a_{1}=4a_{2}$ . But then, dividing both sides of this by 4 allows us to conclude that $a_{1}=a_{2}$ . This is sufficient to prove that this function is one-to-one.

On the other hand, the function $g:{\Bbb R}\longrightarrow {\Bbb R}$ defined by $g(x)=x^{2}$ is not one-to-one since, for example, $g(-2)=4=g(2)$ .

Definition of Onto (Surjective) and Examples

Definition 1.9.2: A function $f:A\longrightarrow B$ is onto (surjective) if every element of $B$ is an output of some input from $A$ . That is, $f$ is onto if for all $b\in B$ , there exists (at least one) $a\in A$ such that $b=f(a)$ .

The function $f:{\Bbb R}\longrightarrow {\Bbb R}$ defined by $f(x)=4x-5$ is surjective. Given $y\in {\Bbb R}$ , the number $x=\frac{y+5}{4}$ has the property that $f(x)=y$ . Here are the details: $f\left(\frac{y+5}{4}\right)=4\left(\frac{y+5}{4}\right)-5=y+5-5=y$ .

It is no accident that $f^{-1}(y)=\frac{y+5}{4}$ .

On the other hand, the function $g:{\Bbb R}\longrightarrow {\Bbb R}$ defined by $g(x)=x^{2}$ is not onto since $g(x)\geq 0$ for all $x\in {\Bbb R}$ . There are no inputs in ${\Bbb R}$ that give negative outputs.

We can “force” $g$ to be onto by restricting its codomain. Do this by defining the codomain to be $[0,\infty)$ instead of ${\Bbb R}$ .

The function $g:{\Bbb R}\longrightarrow [0,\infty)$ defined by $g(x)=x^{2}$ is onto. Given $y\in [0,\infty)$ , the two numbers $x=\pm\sqrt{y}$ both have the property that $g(x)=y$ (of course, when $y=0$ this is actually only one number).

Inverse Functions

Let $f:A\longrightarrow B$ be a one-to-one and onto function (a “bijection”). Then, given any $b\in B$ , there must be a unique element $a\in A$ such that $f(a)=b$ . The existence of this element is guaranteed by the fact that $f$ is onto. The uniqueness of this element is guaranteed by the fact that $f$ is one-to-one.

We have essentially just defined $f^{-1}$ . To be precise, define $f^{-1}:B\longrightarrow A$ by saying, for each $b\in B$ , that $f^{-1}(b)$ is the unique element of $A$ that gets mapped to $b$ . Alternatively, $f^{-1}(b)\in A$ is the unique element of $A$ such that $(f\circ f^{-1})(b)=f(f^{-1}(b))=b$ .

Does this “undoing action” work the other way around? Given $a\in A$ , we know that $f(a)\in B$ . By definition, $f^{-1}(f(a))$ is the unique element of $A$ that gets mapped to $f(a)$ . But we already know that $a$ gets mapped to $f(a)$ ! Therefore, $(f^{-1}\circ f)(a)=f^{-1}(f(a))=a$ .

When $f:A\longrightarrow B$ is one-to-one and onto, we have just seen that $f^{-1}:B\longrightarrow A$ can be defined. We say that $f$ is invertible in this situation.

Also note that if $I_{A}:A\longrightarrow A$ and $I_{B}:B\longrightarrow B$ are the functions defined by $I_{A}(a)=a$ for all $a\in A$ and $I_{B}(b)=b$ for all $b\in B$ , then $f^{-1}\circ f=I_{A}$ and $f\circ f^{-1}=I_{B}$ when $f$ is invertible. The functions $I_{A}$ and $I_{B}$ are called the identity mappings on $A$ and $B$ , respectively.

These last couple equations are analogous to the equations $a^{-1}\cdot a=a\cdot a^{-1}=1$ for nonzero numbers $a\in {\Bbb R}$ . The function $I_{A}$ , for example, is analogous to the number 1 in the sense that $I_{A}\circ h=h\circ I_{A}=h$ for any function $h:A\longrightarrow A$ . This is analogous to the fact that $1\cdot a=a\cdot 1=a$ for any $a\in {\Bbb R}$ .

These ideas can certainly be confusing for many people. Make sure you completely understand everything before moving on.

The Inverse Matrix of an Invertible Linear Transformation

In Section 1.7, “High-Dimensional Linear Algebra”, we saw that a linear transformation $T:{\Bbb R}^{n}\longrightarrow {\Bbb R}^{m}$ can be represented by an $m\times n$ matrix $B$ . This means that, for each input ${\bf x}\in {\Bbb R}^{n}$ , the output $T({\bf x})\in {\Bbb R}^{m}$ can be computed as the product $B{\bf x}$ .

To do this, we define $B{\bf x}$ as a linear combination.

$B{\bf x}=\left[{\bf b}_{1}\ {\bf b}_{2}\ \cdots\ {\bf b}_{n}\right]\left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right]=x_{1}{\bf b}_{1}+x_{2}{\bf b}_{2}+\cdots+x_{n}{\bf b}_{n}\in {\Bbb R}^{m}$ .

Then, in Section 1.8, “Matrix Multiplication and Composite Transformations”, we saw that if $S:{\Bbb R}^{m}\longrightarrow {\Bbb R}^{\ell}$ is a linear transformation, then $S\circ T:{\Bbb R}^{n}\longrightarrow {\Bbb R}^{\ell}$ can be represented by the product of two matrices.

Assuming that $A$ is the $\ell\times m$ matrix representing $S$ , then $(S\circ T)({\bf x})=S(T({\bf x}))=A(B{\bf x})=(AB){\bf x}$ , where $AB$ is defined by:

$AB=A\left[{\bf b}_{1}\ {\bf b}_{2}\ \cdots\ {\bf b}_{n}\right]=\left[A{\bf b}_{1}\ A{\bf b}_{2}\ \cdots\ A{\bf b}_{n}\right]$ .

This product is an $\ell\times n$ matrix.

Therefore, we can also write

$(S\circ T)({\bf x})=(AB){\bf x}=\left[A{\bf b}_{1}\ A{\bf b}_{2}\ \cdots\ A{\bf b}_{n}\right]\left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right]$

$=x_{1}A{\bf b}_{1}+x_{2}A{\bf b}_{2}+\cdots+x_{n}A{\bf b}_{n}\in {\Bbb R}^{\ell}$ .

A Necessary Condition for Invertibility

Evidently, if $S$ and $T$ are to have a “chance” to be inverse functions, and for $A$ and $B$ to be inverse matrices, it must be the case that $n=m=\ell$ . This is indeed the case. In this situation, the resulting matrices are called square matrices because they have a “square shape” (rather than a general “rectangular shape”).

Let’s start by considering inverse linear transformations and inverse matrices in low dimensions.

Application of Inverse Transformations and Inverse Matrices

As with general inverse functions, inverse linear transformations and their corresponding inverse matrices can help us solve infinitely many problems at once. If $T:{\Bbb R}^{n}\longrightarrow {\Bbb R}^{n}$ is an invertible linear transformation with invertible matrix representative $A$ , then we can then solve the general problem $T({\bf x})={\bf b}$ for any ${\bf b}\in {\Bbb R}^{n}$ .

In fact, we can write the answers to these infinitely many problems in one equation as ${\bf x}=T^{-1}({\bf b})=A^{-1}{\bf b}$ . It is therefore useful to find a formula for $T^{-1}$ by finding $A^{-1}$ .

The Inverse Matrix of an Invertible Linear Transformation ${\Bbb R}\longrightarrow {\Bbb R}$

We have seen that a linear transformation $T:{\Bbb R}\longrightarrow {\Bbb R}$ has a formula of the form $T(x)=ax$ for some $a\in {\Bbb R}$ . With matrix notation, we can also write this as $T([x])=[a][x]$ .

Clearly such a function is one-to-one and onto, and hence invertible, if and only if $a\not=0$ . Just as clear, the inverse function in that situation will be $T^{-1}(x)=\frac{x}{a}=\frac{1}{a}x=a^{-1}x$ . This can also be written as $T^{-1}([x])=[a^{-1}][x]$ .

For confirmation of this fact, note that $(T\circ T^{-1})(x)=T(T^{-1}(x))=T(a^{-1}x)=a(a^{-1}x)=(aa^{-1})x=1\cdot x=x$

Because of this, when $a\not=0$ , we say that the inverse matrix of the $1\times 1$ matrix $[a]$ is the $1\times 1$ matrix $[a^{-1}]=\left[\frac{1}{a}\right]$ .

We also write this as $[a]^{-1}=[a^{-1}]$ when $a\not=0$ . In words, this equation says that the inverse matrix of $[a]$ is the matrix $[a^{-1}]=\left[\frac{1}{a}\right]$ when $a\not=0$ .

By definition of a $1\times 1$ matrix times another $1\times 1$ matrix, we can also see that $[a][a]^{-1}=[a]^{-1}[a]=[1]$ . The matrix $[1]$ is called the $1\times 1$ identity matrix. Note that $[1][b]=[b][1]=[b]$ for any $b\in {\Bbb R}$ .

If $a=0$ , then $[a]$ (and $a$ ) has no multiplicative inverse. We say that $[a]$ is noninvertible (or “not invertible”) when $a=0$ .

In the end, $[0]$ is the only noninvertible $1\times 1$ matrix.

The Inverse Matrix of an Invertible Linear Transformation ${\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$

A linear transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ has a formula of the form $T({\bf x})=A{\bf x}$ for some $2\times 2$ matrix $A$ , say $A=\left[\begin{array}{cc} a & b \\ c & d \end{array}\right]$ , where ${\bf x}=\left[\begin{array}{c} x_{1} \\ x_{2} \end{array}\right]$ .

If $T$ is invertible, and assuming that $T^{-1}$ is a linear transformation (which we will prove in the general case further below), then $T^{-1}$ will have a matrix representative as well.

Let us suggestively call this matrix $A^{-1}$ and write $A^{-1}=\left[\begin{array}{cc} \alpha & \beta \\ \gamma & \delta \end{array}\right]$ . One of our goals is to determine how the entries of $A^{-1}$ depend on the entries of $A$ . Another goal is to see what conditions on the entries of $A$ are required for $A$ (and $T$ ) to be invertible.

Before doing so, we first note the truth of the following equation:

$\left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{c} x_{1} \\ x_{2} \end{array}\right]=x_{1}\left[\begin{array}{c} 1 \\ 0 \end{array}\right]+x_{2}\left[\begin{array}{c} 0 \\ 1 \end{array}\right]=\left[\begin{array}{c} x_{1} \\ x_{2} \end{array}\right]$ .

Because of this, we say that $I_{2}=\left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]$ is the $2\times 2$ identity matrix. It has the property that $I_{2}{\bf x}={\bf x}$ for all ${\bf x}\in {\Bbb R}^{2}$ . You can check that it also has the property that $I_{2}B=BI_{2}=B$ for any $2\times 2$ matrix $B$ .

If $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ is invertible with inverse $T^{-1}$ , then $T(T^{-1}({\bf x}))=T^{-1}(T({\bf x}))=I_{{\Bbb R}^{2}}({\bf x})={\bf x}$ for all ${\bf x}\in {\Bbb R}^{2}$ . The function $I_{{\Bbb R}^{2}}:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ is the identity mapping on ${\Bbb R}^{2}$ . Its matrix is $I_{2}$ .

Since $T(T^{-1}({\bf x}))=A(A^{-1}{\bf x})=(AA^{-1}){\bf x}=I_{2}{\bf x}$ and $T^{-1}(T({\bf x}))=A^{-1}(A{\bf x})=(A^{-1}A){\bf x}=I_{2}{\bf x}$ , it follows that we want $AA^{-1}=A^{-1}A=I_{2}$ . This is the key equation to help us find $A^{-1}$ .

Using the Key Equation

Below we show the equation $AA^{-1}=I_{2}$ in terms of the entries of the matrices:

$\left[\begin{array}{cc} a & b \\ c & d \end{array}\right]\left[\begin{array}{cc} \alpha & \beta \\ \gamma & \delta \end{array}\right]=\left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]$ .

Now multiply the matrices on the left to get:

$\left[\begin{array}{cc} a\alpha+b\gamma & a\beta+b\delta \\ c\alpha+d\gamma & c\beta+d\delta \end{array}\right]=\left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]$ .

If we think of $a,b,c,$ and $d$ as given, this is equivalent to a system of four linear equations in four unknowns ( $\alpha,\beta,\gamma,$ and $\delta$ ).

$\begin{cases}\begin{array}{ccccccccc} a\alpha & & & + & b\gamma & & & = & 1 \\ & & a\beta & & & + & b\delta & = & 0 \\ c\alpha & & & + & d\gamma & & & = & 0 \\ & & c\beta & & & + & d\delta & = & 1 \end{array}\end{cases}$

This system is “decoupled” (a.k.a. “uncoupled”). The first and third equations only involve $\alpha$ and $\gamma$ while the second and fourth only involve $\beta$ and $\delta$ . We can therefore think of this as two separate systems of two equations and two unknowns:

$\begin{cases}\begin{array}{ccccc} a\alpha & + & b\gamma & = & 1 \\ c\alpha & + & d\gamma & = & 0 \end{array} \end{cases}\mbox{ and\ \ }\begin{cases}\begin{array}{ccccc} a\beta & + & b\delta & = & 0 \\ c\beta & + & d\delta & = & 1 \end{array} \end{cases}$

Using Row Operations to RREF to Find 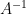$A^{-1}$

We could do row operations on the following two augmented matrices to solve these two systems (the first system for $\alpha$ and $\gamma$ and the second system for $\beta$ and $\delta$ ).

$\left[\begin{array}{ccc} a & b & 1 \\ c & d & 0\end{array} \right]\mbox{ and\ \ } \left[\begin{array}{ccc} a & b & 0 \\ c & d & 1\end{array} \right]$

However, it is more efficient to perform row operations to reduced row echelon form (RREF) on the single “doubly-augmented” matrix shown below.

$\left[\begin{array}{cccc} a & b & 1 & 0 \\ c & d & 0 & 1 \end{array}\right]$

Note that the third column $\left[\begin{array}{c} 1 \\ 0 \end{array}\right]$ represents numbers on the right-hand sides of the equations in the first system above. The fourth column $\left[\begin{array}{c} 0 \\ 1 \end{array}\right]$ represents numbers on the right-hand sides of the equations in the second system above. This matrix is often written in “block” form as $[A\ I_{2}]$ , where $A$ and $I_{2}$ are thought of as “submatrices” of the entire matrix.

Just make sure you realize that the unknowns “switch” depending on which system you are focused on solving.

Details of the Row Operations

Here are the details of the elementary row operations. While doing these calculations, we assume, for the sake of convenience, that we are never dividing by zero. Obviously, there will be some situations where we would not be able to complete this calculation because of division by zero.

$\left[\begin{array}{cccc} a & b & 1 & 0 \\ c & d & 0 & 1 \end{array}\right]\xrightarrow{\frac{1}{a}R_{1}\rightarrow R_{1}}\left[\begin{array}{cccc} 1 & \frac{b}{a} & \frac{1}{a} & 0 \\ c & d & 0 & 1 \end{array}\right]\xrightarrow{-cR_{1}+R_{2}\rightarrow R_{2}}\left[\begin{array}{cccc} 1 & \frac{b}{a} & \frac{1}{a} & 0 \\ 0 & \frac{ad-bc}{a} & -\frac{c}{a} & 1 \end{array}\right]$

Continuing,

$\left[\begin{array}{cccc} 1 & \frac{b}{a} & \frac{1}{a} & 0 \\ 0 & \frac{ad-bc}{a} & -\frac{c}{a} & 1 \end{array}\right]\xrightarrow{\frac{a}{ad-bc}R_{2}\rightarrow R_{2}}\left[\begin{array}{cccc} 1 & \frac{b}{a} & \frac{1}{a} & 0 \\ 0 & 1 & -\frac{c}{ad-bc} & \frac{a}{ad-bc} \end{array}\right]$ .

Finally,

$\left[\begin{array}{cccc} 1 & \frac{b}{a} & \frac{1}{a} & 0 \\ 0 & 1 & -\frac{c}{ad-bc} & \frac{a}{ad-bc} \end{array}\right]\xrightarrow{-\frac{b}{a}R_{2}+R_{1}\rightarrow R_{1}}\left[\begin{array}{cccc} 1 & 0 & \frac{d}{ad-bc} & -\frac{b}{ad-bc} \\ 0 & 1 & -\frac{c}{ad-bc} & \frac{a}{ad-bc} \end{array}\right]$ .

This last step is dependent on the symbolic calculation $-\frac{b}{a}\cdot -\frac{c}{ad-bc}+\frac{1}{a}=\frac{bc+ad-bc}{a(ad-bc)}=\frac{ad}{a(ad-bc)}=\frac{d}{ad-bc}$ .

This implies that the solution of the first system of two equations and two unknowns is $\alpha=\frac{d}{ad-bc},\ \gamma=-\frac{c}{ad-bc}$ , while the solution of the second system of two equations and two unknowns is $\beta=-\frac{b}{ad-bc},\ \delta=-\frac{a}{ad-bc}$ .

In other words,

$\left[\begin{array}{cc} \alpha & \beta \\ \gamma & \delta \end{array}\right]=A^{-1}=\left[\begin{array}{cc} a & b \\ c & d \end{array}\right]^{-1}=\left[\begin{array}{cc} \frac{d}{ad-bc} & -\frac{b}{ad-bc} \\ -\frac{c}{ad-bc} & \frac{a}{ad-bc} \end{array}\right]$ .

It is common to also write this as

$\left[\begin{array}{cc} \alpha & \beta \\ \gamma & \delta \end{array}\right]=A^{-1}=\left[\begin{array}{cc} a & b \\ c & d \end{array}\right]^{-1}=\frac{1}{ad-bc}\left[\begin{array}{cc} d & -b \\ -c & a \end{array}\right]$ .

In so doing we are assuming that we can multiply matrices by scalars (numbers) just as we can with vectors. This is indeed a valid operation.

Whereas scalar multiplication of a number and a vector is said to be done component-wise, scalar multiplication of a number times a matrix is said to be done entry-wise. These two concepts are essentially equivalent. In fact, matrices can even be thought of as vectors, if we want. For example, it is sometimes fruitful to think of a $2\times 2$ matrix as a four-dimensional vector.

Checking the Answer for the Inverse Matrix

We can always check the answer for the inverse matrix using matrix multiplication. Let’s avoid fractions initially by excluding the $ad-bc$ denominator.

$\left[\begin{array}{cc} a & b \\ c & d \end{array}\right]\left[\begin{array}{cc} d & -b \\ -c & a \end{array}\right]=\left[\begin{array}{cc} ad-bc & -ab+ab \\ cd-cd & -bc+ad \end{array}\right]=\left[\begin{array}{cc} ad-bc & 0 \\ 0 & ad-bc \end{array}\right]$

Multiplying this matrix entry-wise by the scalar $\frac{1}{ad-bc}$ yields the identity matrix $I_{2}$ , as desired. Our answer is confirmed.

Condition for Invertibility

The calculations above are dependent on not dividing by zero. In other words, to do them, we are implicitly assuming that $a\not=0$ and $ad-bc\not=0$ .

However, in the end, it turns out that $a$ can be zero, as long as $ad-bc\not=0$ (so $b\not=0$ and $c\not=0$ if $a=0$ ). The formula for $A^{-1}$ in that case turns out to be the same, as it should be because of our checking of the answer in the previous section.

Note that $ad-bc$ is a quantity we have seen before, in Section 1.5, “Matrices and Linear Transformations in Low Dimensions”. It is the determinant of the matrix $A=\left[\begin{array}{cc} a & b \\ c & d \end{array}\right]$ , denoted by $\det(A)=ad-bc$ .

These observations are important enough to be summarized and labeled as a theorem.

Theorem 1.9.1: A $2\times 2$ matrix $A=\left[\begin{array}{cc} a & b \\ c & d \end{array}\right]$ is invertible if and only if the determinant $\det(A)=ad-bc\not=0$ . Because of this, a linear transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ is invertible if and only if its (standard) matrix has a nonzero determinant.

Using the Inverse Matrix

With the formula for our $2\times 2$ inverse matrix in hand, we can very quickly solve an arbitrary system of two equations and two unknowns when there is a unique solution. The arbitrary system can be written both in scalar form and in matrix/vector form.

$\begin{cases}\begin{array}{ccccc} ax & + & by & = & u \\ cx & + & dy & = & v \end{array}\end{cases}\mbox{ or\ \ \ }\left[\begin{array}{cc} a & b \\ c & d \end{array}\right]\left[\begin{array}{c} x \\ y \end{array}\right]=\left[\begin{array}{c} u \\ v \end{array}\right]\Leftrightarrow A{\bf x}={\bf b}$

When $\det(A)=ad-bc\not=0$ , for any fixed vector ${\bf b}$ , the unique solution of the system is

${\bf x}=A^{-1}{\bf b}=\frac{1}{ad-bc}\left[\begin{array}{cc} d & -b \\ -c & a \end{array}\right]\left[\begin{array}{c} u \\ v \end{array}\right]=\left[\begin{array}{c} \frac{du-bv}{ad-bc} \\ \frac{-cu+av}{ad-bc} \end{array}\right]$ .

This can be checked by substitution into the original system. In fact, now that we have notation for the identity matrix, we can also check it via a more abstract substitution and the associative property of matrix multiplication: $A(A^{-1}{\bf b})=(AA^{-1}){\bf b}=I{\bf b}={\bf b}$ . For this example, $I$ would be the $2\times 2$ identity matrix. However, this abstract calculation works in any dimension.

The last calculation confirms that the vector $A^{-1}{\bf b}$ is a solution of the equation $A{\bf x}={\bf b}$ when $A$ is invertible. The following calculations confirm that $A^{-1}{\bf b}$ is the only possible solution when $A$ is invertible.

$A{\bf x}={\bf b}\Rightarrow A^{-1}(A{\bf x})=A^{-1}{\bf b}\Rightarrow {\bf x}=I{\bf x}=(A^{-1}A){\bf x}=A^{-1}(A{\bf x})=A^{-1}{\bf b}$

The Inverse Matrix of an Invertible Linear Transformation ${\Bbb R}^{3}\longrightarrow {\Bbb R}^{3}$

For a linear transformation in three dimensions, let’s start with a couple particular examples rather than the general case.

An Invertible Example

Suppose $T:{\Bbb R}^{3}\longrightarrow {\Bbb R}^{3}$ is defined by:

$T({\bf x})=A{\bf x}=\left[\begin{array}{ccc} 4 & -2 & 3 \\ -1 & 5 & 6 \\ 3 & -3 & 4 \end{array}\right]\left[\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}\right]=\left[\begin{array}{c} 4x_{1}-2x_{2}+3x_{3} \\ -x_{1}+5x_{2}+6x_{3} \\ 3x_{1}-3x_{2}+4x_{3} \end{array}\right]$ .

If it exists, the inverse matrix of $A$ would be of the form $A^{-1}=\left[\begin{array}{ccc} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{array}\right]$ and we would seek to solve 3 uncoupled systems of 3 equations and 3 unknowns each.

$\begin{cases}\begin{array}{c} 4b_{11}-2b_{21}+3b_{31}=1 \\ -b_{11}+5b_{21}+6b_{31}=0 \\ 3b_{11}-3b_{21}+4b_{31}=0\end{array} \end{cases}\mbox{and\ }\begin{cases}\begin{array}{c} 4b_{12}-2b_{22}+3b_{32}=0 \\ -b_{12}+5b_{22}+6b_{32}=1 \\ 3b_{12}-3b_{22}+4b_{32}=0\end{array} \end{cases}\mbox{and\ }\begin{cases}\begin{array}{c} 4b_{13}-2b_{23}+3b_{33}=0 \\ -b_{13}+5b_{23}+6b_{33}=0 \\ 3b_{13}-3b_{23}+4b_{33}=1\end{array} \end{cases}$

These are most efficiently solved simultaneously by performing row operations on a “triply-augmented” matrix, keeping in mind the unknowns solved for are different for each of the last three columns.

Here is the result for this example. The details are left to you as an exercise.

$\left[\begin{array}{cccccc} 4 & -2 & 3 & 1 & 0 & 0 \\ -1 & 5 & 6 & 0 & 1 & 0 \\ 3 & -3 & 4 & 0 & 0 & 1\end{array}\right]\xrightarrow{\ \ \ RREF\ \ \ }\left[\begin{array}{cccccc} 1 & 0 & 0 & \frac{19}{36} & -\frac{1}{72} & -\frac{3}{8} \\ 0 & 1 & 0 & \frac{11}{36} & \frac{7}{72} & -\frac{3}{8} \\ 0 & 0 & 1 & -\frac{1}{6} & \frac{1}{12} & \frac{1}{4}\end{array}\right]$

Focus on the fourth column. This corresponds to the solution of the first of the three systems of 3 equations and 3 unknowns. The unique solution of that system is $(b_{11},b_{21},b_{31})=\left(\frac{19}{36},\frac{11}{36},-\frac{1}{6}\right)$ .

Likewise, if we focus on the fifth and sixth columns, we obtain the unique solutions of the second and third systems, respectively. The answers are $(b_{12},b_{22},b_{32})=\left(-\frac{1}{72},\frac{7}{72},\frac{1}{12}\right)$ and $(b_{13},b_{23},b_{33})=\left(-\frac{3}{8},-\frac{3}{8},\frac{1}{4}\right)$ .

The Answer and Confirmation Via Multiplication

Combining all this information leads to the conclusion that the inverse matrix of $A$ exists and is

$A^{-1}=\left[\begin{array}{ccc} \frac{19}{36} & -\frac{1}{72} & -\frac{3}{8} \\ \frac{11}{36} & \frac{7}{72} & -\frac{3}{8} \\ -\frac{1}{6} & \frac{1}{12} & \frac{1}{4} \end{array}\right]$ .

We should check this. To help us avoid fractions as much as possible, notice that we can write our answer above as

$A^{-1}=\frac{1}{72}\left[\begin{array}{ccc} 38 & -1 & -27 \\ 22 & 7 & -27 \\ -12 & 6 & 18 \end{array}\right]$

Now multiply the original matrix times this new matrix with the factor of $\frac{1}{72}$ in front. Make sure you use the dot product-related version of matrix multiplication to check this as quickly as possible.

$AA^{-1}=\frac{1}{72}\left[\begin{array}{ccc} 4 & -2 & 3 \\ -1 & 5 & 6 \\ 3 & -3 & 4 \end{array}\right]\left[\begin{array}{ccc} 38 & -1 & -27 \\ 22 & 7 & -27 \\ -12 & 6 & 18 \end{array}\right]$

$=\frac{1}{72}\left[\begin{array}{ccc} 152-44-36 & -4-14+18 & -108+54+54 \\ -38+110-72 & 1+35+36 & 27-135+108 \\ 114-66-48 & -3-21+24 & -81+81+72 \end{array}\right]$ .

And this simplifies to

$=\frac{1}{72}\left[\begin{array}{ccc} 72 & 0 & 0 \\ 0 & 72 & 0 \\ 0 & 0 & 72 \end{array}\right]=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]=I_{3}$ .

As another check, you could confirm that $A^{-1}A=I_{3}$ as well. The details of the calculations are actually different.

Using the Inverse Matrix

We can now use the inverse matrix to solve an arbitrary system of the form

$\begin{cases}\begin{array}{ccccccc} 4x & - & 2y & + & 3z & = & u \\ -x & + & 5y & + & 6z & = & v \\ 3x & - & 3y & + & 4z & = & w \\ \end{array} \end{cases}$ .

The answer is

$\left[\begin{array}{c} x \\ y \\ z \end{array}\right]={\bf x}=A^{-1}{\bf b}=\frac{1}{72}\left[\begin{array}{ccc} 38 & -1 & -27 \\ 22 & 7 & -27 \\ -12 & 6 & 18 \end{array}\right]\left[\begin{array}{c} u \\ v \\ w \end{array}\right]=\left[\begin{array}{c} \frac{19}{36}u-\frac{1}{72}v-\frac{3}{8}w \\ \frac{11}{36}u+\frac{7}{72}v-\frac{3}{8}w \\ -\frac{1}{6}u+\frac{1}{12}v+\frac{1}{4}w \end{array}\right]$

An Non-Invertible Example

Suppose $T:{\Bbb R}^{3}\longrightarrow {\Bbb R}^{3}$ is defined by:

$T({\bf x})=A{\bf x}=\left[\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right]\left[\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}\right]=\left[\begin{array}{c} x_{1}+2x_{2}+3x_{3} \\ 4x_{1}+5x_{2}+6x_{3} \\ 7x_{1}+8x_{2}+9x_{3} \end{array}\right]$ .

The “triply-augmented” matrix we need to row reduce is again of the general form $[A\ \ I_{3}]$ . Here is the result.

$\left[\begin{array}{cccccc} 1 & 2 & 3 & 1 & 0 & 0 \\ 4 & 5 & 6 & 0 & 1 & 0 \\ 7 & 8 & 9 & 0 & 0 & 1\end{array}\right]\xrightarrow{\ \ \ RREF\ \ \ }\left[\begin{array}{cccccc} 1 & 0 & -1 & 0 & -\frac{8}{3} & \frac{5}{3} \\ 0 & 1 & 2 & 0 & \frac{7}{3} & -\frac{4}{3} \\ 0 & 0 & 0 & 1 & -2 & 1 \end{array}\right]$

The third row has all zeros in the first three columns and nonzero numbers in the last three columns. The first three columns correspond to the coefficients of the unknowns of the three systems of 3 equations and 3 unknowns to solve for the entries of $A^{-1}$ . This means that all three systems are inconsistent (the third equations that result from row operations are contradictions: $0=1$ , $0=-2$ , and $0=1$ ).

Therefore, $A^{-1}$ does not exist for this example! This means that $T^{-1}$ also does not exist. The linear transformation $T$ (and its matrix $A$ ) are noninvertible.

Since $A$ is noninvertible, this also means the solutions of $A{\bf x}={\bf b}$ , if there are any, cannot be written in terms of an inverse matrix.

In the end, we will see that, for this example, such a system is consistent for some vectors ${\bf b}\in {\Bbb R}^{3}$ and inconsistent for other such vectors. When the system is consistent, there will be infinitely many solutions.

These facts correspond to the fact that, for this example, the linear transformation $T:{\Bbb R}^{3}\longrightarrow {\Bbb R}^{3}$ defined by $T({\bf x})=A{\bf x}$ is neither one-to-one nor onto. Its kernel (null space of $A$ ) contains more than the zero vector and the image (column space of $A$ ) is not all of ${\Bbb R}^{3}$ .

Determinant Condition for Three-Dimensional Square Matrices

Is there a determinant condition for linear transformations $T:{\Bbb R}^{3}\longrightarrow {\Bbb R}^{3}$ ? Yes, there is.

We start by stating the very complicated formula for the determinant of a $3\times 3$ matrix. This formula should not be memorized. Instead, there are techniques for computation that are worth remembering. We will reserve those techniques for the next section.

$\det(A)=\det\left(\left[\begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i\end{array}\right]\right)=a(ei-fh)-b(di-fg)+c(dh-eg)$

And here is the determinant condition.

Theorem 1.9.2: A $3\times 3$ matrix $A=\left[\begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array}\right]$ is invertible if and only if the determinant $\det(A)=a(ei-fh)-b(di-fg)+c(dh-eg)\not=0$ . Because of this, a linear transformation $T:{\Bbb R}^{3}\longrightarrow {\Bbb R}^{3}$ is invertible if and only if its (standard) matrix has a nonzero determinant.

Referring to the examples above, notice that $\det\left(\left[\begin{array}{ccc} 4 & -2 & 3 \\ -1 & 5 & 6 \\ 3 & -3 & 4 \end{array}\right]\right)=4(20+18)-(-2)(-4-18)+3(3-15)$

$=152-44-36=72\not=0$

while

$\det\left(\left[\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right]\right)=1(45-48)-(2)(36-42)+3(32-35)=-3+12-9=0$ .

The General Case

Suppose $T:{\Bbb R}^{n}\longrightarrow {\Bbb R}^{n}$ is a linear transformation with (standard) $T({\bf x})=A{\bf x}$ for some $n\times n$ square matrix $A$ . There are three issues to consider.

If $T$ is an invertible function, is $T^{-1}$ a linear transformation? (We have been assuming this to be true so far.)
If $T$ is invertible (so that $A$ is invertible) and $T^{-1}$ is linear, how is $A^{-1}$ found so that $T^{-1}({\bf y})=A^{-1}{\bf y}$ ?
Is there a determinant condition on $A$ to decide the invertibility of both $A$ and $T$ ?

The answer to (3) is “yes”. We will leave our exploration of this fact for the next section.

The Inverse of an Invertible Linear Transformation is a Linear Transformation

The answer to (1) is “yes”. Verifying this is trickier than you might think. Given scalars $a,b\in {\Bbb R}$ and vectors ${\bf u},{\bf v}\in {\Bbb R}^{n}$ , we need to prove that $T^{-1}$ is operation-preserving. That is, we need to prove that

$T^{-1}(a{\bf u}+b{\bf v})=aT^{-1}({\bf u})+bT^{-1}({\bf v})$ .

To demonstrate this, we use the facts that $T$ and $T^{-1}$ are inverses, that $T$ is linear (operation-preserving), and that $T$ is one-to-one when it is invertible. First, since $T$ and $T^{-1}$ are inverses,

$T(T^{-1}(a{\bf u}+b{\bf v}))=a{\bf u}+b{\bf v}$ .

Next, for the same reason, and since $T$ is linear (operation-preserving),

$T(aT^{-1}({\bf u})+bT^{-1}({\bf v}))=aT(T^{-1}({\bf u}))+bT(T^{-1}({\bf v}))=a{\bf u}+b{\bf v}$ .

Therefore, $T(T^{-1}(a{\bf u}+b{\bf v}))=T(aT^{-1}({\bf u})+bT^{-1}({\bf v}))$ .

But now the fact that $T$ is one-to-one implies that $T^{-1}(a{\bf u}+b{\bf v})=aT^{-1}({\bf u})+bT^{-1}({\bf v})$ . This is exactly what we set out to prove.

Algorithm for Finding the Inverse Matrix of an Invertible Linear Transformation

The algorithm (method) of finding $A^{-1}$ , as well as determining its invertibility, is completely analogous to what we did in the two and three-dimensional cases above.

Form the augmented matrix $[A\ \ I_{n}]$ and use elementary row operations to obtain its reduced row echelon form (RREF).

If the block form of the result is $[I_{n}\ \ B]$ , then $A$ is invertible and $A^{-1}=B$ .

If the block form of the result contains a row of $n$ zeros in the first $n$ columns, then $A$ is noninvertible.

This method is justified because we are solving a $n$ systems of $n$ linear equations in $n$ unknowns, and each column of $I_{n}$ on the right side of the original augmented matrix $[A\ \ I_{n}]$ represents the right-hand side of one of these systems. These right hand sides consist of one “1” and $n-1$ “0’s”, based on the key equation $AA^{-1}=I_{n}$ .

A Visual Example (Inverse of a Rotation)

We end this section with a visual two-dimensional example. It demonstrates that the inverse of a $90^{\circ}$ counterclockwise rotation about the origin is a $90^{\circ}$ clockwise rotation about the origin. This can also be thought of as a $270^{\circ}$ counterclockwise rotation, but the first interpretation is more natural.

Let $R:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ be a $90^{\circ}$ counterclockwise rotation about the origin. In Section 1.8, “Matrix Multiplication and Composite Transformations”, we saw that

$R({\bf x})=A{\bf x}=\left[\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right]\left[\begin{array}{c} x_{1} \\ x_{2} \end{array}\right]=\left[\begin{array}{c} -x_{2} \\ x_{1} \end{array}\right]$ .

Here are the steps of the row-reduction algorithm on the augmented matrix $[A\ \ I_{2}]$ :

$\left[\begin{array}{cccc} 0 & -1 & 1 & 0 \\ 1 & 0 & 0 & 1 \end{array}\right]\xrightarrow{R_{1}\leftrightarrow R_{2}}\left[\begin{array}{cccc} 1 & 0 & 0 & 1 \\ 0 & -1 & 1 & 0 \end{array}\right]\xrightarrow{(-1)R_{2}\rightarrow R_{2}}\left[\begin{array}{cccc} 1 & 0 & 0 & 1 \\ 0 & 1 & -1 & 0 \end{array}\right]$

This is in the block form $[I_{2}\ \ B]$ , so $A^{-1}=B=\left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right]$ .

The function $R^{-1}({\bf y})=A^{-1}{\bf y}=\left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right]\left[\begin{array}{c} y_{1} \\ y_{2} \end{array}\right]=\left[\begin{array}{c} y_{2} \\ -y_{1} \end{array}\right]$ does indeed represent a $90^{\circ}$ clockwise rotation about the origin.

This is visualized in the animation below. We see both the action of $R$ and $R^{-1}$ in this animation.

*The action of $R$ rotates counterclockwise by $90^{\circ}$ while the action of $R^{-1}$ rotates clockwise by $90^{\circ}$ .*

It is also interesting to note that the inverse of a shear will be a shear in the “opposite direction” while the inverse of a reflection will be itself.

Exercises

(a) Show all the details of the row operations necessary on the block augmented matrix $[A\ \ I_{3}]$ to confirm that the inverse matrix of $A=\left[\begin{array}{ccc} 4 & -2 & 3 \\ -1 & 5 & 6 \\ 3 & -3 & 4 \end{array}\right]$ is $A^{-1}=\left[\begin{array}{ccc} \frac{19}{36} & -\frac{1}{72} & -\frac{3}{8} \\ \frac{11}{36} & \frac{7}{72} & -\frac{3}{8} \\ -\frac{1}{6} & \frac{1}{12} & \frac{1}{4} \end{array}\right]$ . (b) Confirm that $AA^{-1}=I_{3}$ by direct multiplication.
Let $T:{\Bbb R}^{4}\longrightarrow {\Bbb R}^{4}$ be defined by $T({\bf x})=A{\bf x}=\left[\begin{array}{cccc} 1 & 2 & -5 & 3 \\ 2 & 2 & 0 & -4 \\ -1 & 0 & 2 & 5 \\ 4 & -3 & -3 & 1 \end{array}\right]\left[\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{array}\right]=\left[\begin{array}{c} x_{1}+2x_{2}-5x_{3}+3x_{4} \\ 2x_{1}+2x_{2}-4x_{4} \\ -x_{1}+2x_{3}+5x_{4} \\ 4x_{1}-3x_{2}-3x_{3}+x_{4} \end{array}\right]$ . Find a formula for $T^{-1}$ or confirm that $T^{-1}$ does not exist. If $T^{-1}$ exists, write a simplified formula for the solution of the general system $T({\bf x})=A{\bf x}={\bf b}$ , where ${\bf b}=\left[\begin{array}{c}b_{1}\\b_{2}\\b_{3}\\b_{4}\end{array}\right]$ .

Video for Section 1.9

Here’s a video overview of the content of Section 1.9.