High-Dimensional Linear Algebra - Infinity is Really Big

Visual Linear Algebra Online, Section 1.7

Many practical situations that require the use of linear algebra can involve hundreds or even thousands of unknowns. Modeling a national economy, optimizing the purchase of supplies, and managing flight schedules are prominent examples.

A vector quantity representing all the data in such a situation might therefore have hundreds or thousands of components. This is a difficult-to-imagine, but common, situation in high-dimensional linear algebra. How in the world can we visualize such a vector? Is it worth even trying to visualize it in some way?

A Least Squares Problem

A data-fitting problem might just have two variables and be easy to visualize at the start, but it could have many equations. This can lead to visualization difficulties as we try to conceptualize the best solution of the problem.

For example, suppose we want to find the “line of best fit” for the five data points $(1,4), (2, 3), (3,3), (4,2)$ , and $(5,0)$ .

These points, along with the line of best fit, are shown in the figure below. The line of best fit has equation $y=f(x)=-0.9x+5.1$ . The vertical lines represent the “errors” in using the line to approximate the $y$ -coordinates of the data values at the given $x$ -values.

A least squares (line of best fit) problem leads to a need for high-dimensional linear algebra. — The data points and the line of best fit (a.k.a. the least squares line or the line of regression). The signed distances of the vertical lines are the errors in using the line to estimate the $y$ -coordinates of the data points.

The data points and the line of best fit (a.k.a. the least squares line or the line of regression). The signed distances of the vertical lines are the errors in using the line to estimate the $y$ -coordinates of the data points.

The most common way to find this line is called the Method of Least Squares. Assume that the line has equation $y=f(x)=mx+b$ for some constants $m$ and $b$ . The goal is to choose the values of $m$ and $b$ to minimize the sum of the squares of the errors between the $y$ -coordinates of the data and the corresponding $y$ -coordinates along the line. In the picture above, the sum of the squares of the lengths of the brown lines is what is minimized by the location (defined by the slope and intercept) of the blue line.

This problem can be solved with calculus. It can also be solved with linear algebra.

The Corresponding Overdetermined System

Pretend, at the outset, that the graph of the line goes exactly through all five points. Then errors would be zero. In fact, this would be equivalent to the following linear system of 5 equations and 2 unknowns having a unique solution.

$\begin{cases}\begin{array}{c} m+b=4 \\ 2m+b=3 \\ 3m+b=3 \\ 4m+b=2 \\ 5m+b=0 \end{array} \end{cases}$

But this system has no solution. It is said to be overdetermined. This is typical when there are more equations than unknowns. If we graph these five lines in an $mb$ -plane, there is no point of common intersection.

The graphs of these five lines is shown below. The black point $(m,b)=(-.9,5.1)$ has coordinates equal to the slope and intercept of the line of best fit above. In the new picture below, this point somehow represents the point that is “closest” to being the common intersection of the five lines. It might be thought of as some kind of “average” of the red points at the intersections of pairs of these lines. Note that the point $(m,b)=(-1,5)$ is the intersection of more than one pair of these lines.

The five lines from the system of 5 equations and 2 unknowns above. There is no point of common intersection for all the lines. The black point is a kind of ‘averaged solution’ and corresponds to the least squares solution to the original data-fitting problem.

The Corresponding Linear Transformation

Here again is our overdetermined system.

$\begin{cases}\begin{array}{c} m+b=4 \\ 2m+b=3 \\ 3m+b=3 \\ 4m+b=2 \\ 5m+b=0 \end{array} \end{cases}$

We can think of the left-hand sides of these equations as defining a linear transformation. Let ${\Bbb R}^{5}$ represent five-dimensional space. This cannot be visualized, but it can be conceptualized as the collection of all five-dimensional column vectors ( $5\times 1$ real matrices). Define $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{5}$ by the following formula, for ${\bf x}=\left[\begin{array}{c} m \\ b \end{array}\right]$ .

$T({\bf x})=T\left(\left[\begin{array}{c} m \\ b \end{array}\right]\right)=\left[\begin{array}{c} m+b \\ 2m+b \\ 3m+b \\ 4m+b \\ 5m+b \end{array}\right]=m\left[\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ 5 \end{array}\right]+b\left[\begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{array}\right]$

The expression on the right side of the preceding line is a linear combination of two five-dimensional vectors. By what we have emphasized in both Section 1.5, “Matrices and Linear Transformations in Low Dimensions” and Section 1.6, “Linear Algebra in Three Dimensions”, we can write the linear transformation as a matrix multiplication $A{\bf x}$ . The two five-dimensional vectors are the columns of $A$ . The components of ${\bf x}$ , the scalars $m$ and $b$ , are the corresponding weights.

In other words, we can write the following equation.

$T({\bf x})=A{\bf x}=\left[\begin{array}{cc} 1 & 1 \\ 2 & 1 \\ 3 & 1 \\ 4 & 1 \\ 5 & 1 \end{array}\right]\left[\begin{array}{c} m \\ b \end{array}\right]=m\left[\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ 5 \end{array}\right]+b\left[\begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{array}\right]=\left[\begin{array}{c} m+b \\ 2m+b \\ 3m+b \\ 4m+b \\ 5m+b \end{array}\right]$

The Image of T (Column Space of A)

Since the columns of $A$ are not scalar multiples of each other, the image of $T$ (the column space of $A$ ) will be a two-dimensional plane through the origin sitting inside five-dimensional space. Of course, this is impossible to visualize, other than by analogy of a two-dimensional plane sitting inside three-dimensional space. But $T$ is clearly not an onto function.

In particular, the five-dimensional vector ${\bf v}=\left[\begin{array}{c} 4 \\ 3 \\ 3 \\ 2 \\ 0 \end{array}\right]$ representing the right-hand sides of the original system is not an element of $\mbox{Im}(T)=\mbox{Col}(A)=\{T({\bf x})\, |\, {\bf x}\in {\Bbb R}^{2}\}=\{A{\bf x}\, |\, {\bf x}\in {\Bbb R}^{2}\}\subseteq {\Bbb R}^{5}$ .

But we should not expect it to “typically” be the case that such a vector will be in the image. If we choose other numbers, at random, for the $y$ -coordinates of our original data points, the resulting vector ${\bf v}$ is unlikely to be in the two-dimensional plane $\mbox{Im}(T)=\mbox{Col}(A)$ sitting inside five-dimensional space. After all, five-dimensional space is intuitively a lot “bigger” than any two-dimensional “subspace”.

On the other hand, the vector $T\left(\left[\begin{array}{c} -0.9 \\ 5.1 \end{array}\right]\right)=\left[\begin{array}{cc} 1 & 1 \\ 2 & 1 \\ 3 & 1 \\ 4 & 1 \\ 5 & 1 \end{array}\right]\left[\begin{array}{c} -0.9 \\ 5.1 \end{array}\right]=\left[\begin{array}{c} 4.2 \\ 3.3 \\ 2.4 \\ 1.5 \\ 0.6 \end{array}\right]$ is an element of $\mbox{Im}(T)=\mbox{Col}(A)$ . In fact, it is the unique element of this two-dimensional subspace of ${\Bbb R}^{5}$ that is closest to the vector ${\bf v}=\left[\begin{array}{c} 4 \\ 3 \\ 3 \\ 2 \\ 0 \end{array}\right]$ .

This means that, for all possible values of $m$ and $b$ that could have been chosen and all possible corresponding inputs ${\bf x}=\left[\begin{array}{c} m \\ b \end{array}\right]$ of $T$ , the magnitude $||T({\bf x})-{\bf v}||=||A{\bf x}-{\bf v}||$ is smallest when ${\bf x}=\left[\begin{array}{c} -0.9 \\ 5.1 \end{array}\right]$ . But such a magnitude, as we will see below, is a square root of a sum of squares. This is why this approach is called the Method of Least Squares.

But how is the two-dimensional vector ${\bf x}=\left[\begin{array}{c} -0.9 \\ 5.1 \end{array}\right]$ found? That is a topic for another section.

Visualizing the Least Squares Solution

We can produce a visualization by analogy with the picture below. Pretend that the three-dimensional space shown is actually five-dimensional space. The plane shown represents the two-dimensional subspace $\mbox{Im}(T)=\mbox{Col}(A)$ , while ${\bf v}$ represents the five-dimensional vector. The output $T({\bf x})=A{\bf x}$ is the closest point in the subspace $\mbox{Im}(T)=\mbox{Col}(A)$ , to ${\bf v}$ .

Least squares visualization for high-dimensional linear algebra. — If $T({\bf x})=A{\bf x}\in\mbox{Im}(T)$ is the closest element of $\mbox{Im}(T)$ to ${\bf v}\in {\Bbb R}^{5}$ , then ${\bf x}$ is the least squares solution. Its components give the slope $m$ and intercept $b$ of the line of best fit. This visual is by analogy: $\mbox{Im}(T)=\mbox{Col}(A)$ is a two-dimensional plane through the origin in five-dimensional space ${\Bbb R}^{5}$ .

If $T({\bf x})=A{\bf x}\in\mbox{Im}(T)$ is the closest element of $\mbox{Im}(T)$ to ${\bf v}\in {\Bbb R}^{5}$ , then ${\bf x}$ is the least squares solution. Its components give the slope $m$ and intercept $b$ of the line of best fit. This visual is by analogy: $\mbox{Im}(T)=\mbox{Col}(A)$ is a two-dimensional plane through the origin in five-dimensional space ${\Bbb R}^{5}$ .

Notice the right angle in this picture. Evidently, the notion of an angle can be generalized to higher dimensions, though it can only be visualized by analogy.

n-Dimensional Space 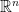${\Bbb R}^{n}$

We see that high-dimensional linear algebra, which we can only visualize by analogy, can evidently still be useful. Let us therefore commence with a discussion of $n$ -dimensional space, where $n$ is any positive integer, no matter how large.

Definitions

An $n$ -dimensional vector is a $n\times 1$ matrix with real number entries. We write it as shown below. The set ${\Bbb R}^{n}$ consists of all possible $n$ -dimensional vectors. The symbol $-{\bf v}$ means $(-1){\bf v}$ and is indeed the additive inverse of ${\bf v}$ .

${\bf x}=\left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right]\mbox{ and } {\Bbb R}^{n}=\left\{\left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right]\, \bigg|\, x_{i}\in {\Bbb R}\mbox{ for all }i=1,2,\ldots,n\right\}$

Of course, as always, vector addition and scalar multiplication is done component-wise. All scalars are assumed to be real numbers.

${\bf x}+{\bf y}=\left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right]+\left[\begin{array}{c} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{array}\right]=\left[\begin{array}{c} x_{1}+y_{1} \\ x_{2}+y_{2} \\ \vdots \\ x_{n}+y_{n}\end{array}\right]$

and

$c{\bf x}=c\left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right]=\left[\begin{array}{c} cx_{1} \\ cx_{2} \\ \vdots \\ cx_{n} \end{array}\right]$

Properties

These definitions allow us to prove all the properties in the theorem below, based on the corresponding properties of real numbers. The proof is easy, though it is also tedious. The zero vector has all $n$ components equal to zero.

Theorem 1.7.1: The following algebra statements are true.

(Closure under Vector Addition) ${\bf u}+{\bf v}\in {\Bbb R}^{n}$ for all ${\bf u},{\bf v}\in {\Bbb R}^{n}$ .
(Commutativity) ${\bf u}+{\bf v}={\bf v}+{\bf u}$ for all ${\bf u},{\bf v}\in {\Bbb R}^{n}$ .
(Associativity of Vector Addition) $({\bf u}+{\bf v})+{\bf w}={\bf u}+({\bf v}+{\bf w})$ for all ${\bf u},{\bf v},{\bf w} \in {\Bbb R}^{n}$ .
(Zero is an Additive Identity) ${\bf u}+{\bf 0}={\bf u}$ for all ${\bf u}\in {\Bbb R}^{n}$ .
(Additive Inverses) ${\bf u}+(-{\bf u})={\bf 0}$ for all ${\bf u}\in {\Bbb R}^{n}$ .
(Closure under Scalar Multiplication) $c{\bf u}\in {\Bbb R}^{n}$ for all $c\in {\Bbb R}$ and for all ${\bf u}\in {\Bbb R}^{n}$ .
(Distributivity of Scalars over Vector Addition) $c({\bf u}+{\bf v})=c{\bf u}+c{\bf v}$ for all $c\in {\Bbb R}$ and for all ${\bf u}, {\bf v}\in {\Bbb R}^{n}$ .
(Distributivity of Vectors over Scalar Addition) $(c+d){\bf u}=c{\bf u}+d{\bf u}$ for all $c,d\in {\Bbb R}$ and for all ${\bf u}\in {\Bbb R}^{n}$ .
(Associativity of Scalar Multiplication) $c(d{\bf u})=(cd){\bf u}$ for all $c,d\in {\Bbb R}$ and for all ${\bf u}\in {\Bbb R}^{n}$ .
(Multiplication by the Scalar 1) $1{\bf u}={\bf u}$ for all ${\bf u}\in {\Bbb R}^{n}$ .

The Dot Product and Angle Between Two Vectors

In high-dimensional linear algebra, the dot product can be defined in a way that is analogous to the two-dimensional case. The following formula is the definition. It is a sum of products of corresponding components.

${\bf x}\cdot {\bf y}=\left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right]\cdot \left[\begin{array}{c} y_{1} \\ y_{2} \\ \vdots \\ y_{n}\end{array}\right]=x_{1}y_{1}+x_{2}y_{2}+\cdots x_{n}y_{n}=\displaystyle\sum_{i=1}^{n}x_{i}y_{i}$

Magnitude and Properties

The magnitude (length) of an $n$ -dimensional vector is then defined to be $||{\bf v}||=\sqrt{{\bf v}\cdot {\bf v}}$ . Perhaps it is better to always call this a “magnitude” rather than a “length”, since it is impossible to imagine literally “measuring” its length in $n$ -dimensions. However, we will not shy away from using either term.

It is easy (but tedious) to prove the first four algebraic properties of dot products in $n$ -dimensions listed below. The fifth one is a bit harder.

Theorem 1.7.2: The following properties are true for given arbitrary vectors in ${\Bbb R}^{n}$ and scalars in ${\Bbb R}$ .

(Commutative Property) ${\bf v}\cdot {\bf w}={\bf w}\cdot {\bf u}$ .
(Distributive Property) ${\bf u}\cdot ({\bf v}+{\bf w})={\bf u}\cdot {\bf v}+{\bf u}\cdot {\bf w}$ .
(Associative Property) $(\lambda {\bf v})\cdot {\bf w}=\lambda({\bf v}\cdot {\bf w})={\bf v}\cdot (\lambda {\bf w})$ .
(Non-negativity) ${\bf v}\cdot {\bf v}\geq 0$ . In addition, ${\bf v}\cdot {\bf v}=0$ if and only if ${\bf v}={\bf 0}$ .
(Triangle Inequality) $||{\bf v}+{\bf w}||\leq ||{\bf v}||+||{\bf w}||$ .

Angle Between Two Vectors

Recall that in Section 1.2, “Vectors in Two Dimensions” and Section 1.6, “Linear Algebra in Three Dimensions“, we saw that the dot product of two vectors is intimately tied to an angle $\theta$ between the two vectors. In particular, we saw that ${\bf v}\cdot {\bf w}=||{\bf v}||\, ||{\bf w}||\, \cos(\theta)$ and therefore $\theta=\arccos\left(\frac{{\bf v}\cdot {\bf w}}{||{\bf v}||\, ||{\bf w}||}\right)=\cos^{-1}\left(\frac{{\bf v}\cdot {\bf w}}{||{\bf v}||\, ||{\bf w}||}\right)$ .

But how do we define an angle between vectors in high-dimensional linear algebra?

Here is a bright idea. Why not use the expression $\arccos\left(\frac{{\bf v}\cdot {\bf w}}{||{\bf v}||\, ||{\bf w}||}\right)=\cos^{-1}\left(\frac{{\bf v}\cdot {\bf w}}{||{\bf v}||\, ||{\bf w}||}\right)$ to do the defining for us?

This is indeed the best thing to do.

There is an issue to clear up, however. Recall that the arccosine (inverse cosine) function is only defined for inputs that are in the interval $[-1,1]=\{x\in {\Bbb R}\, |\, -1\leq x\leq 1\}$ on the real number line. Therefore, to use the expressions in the previous paragraph to define the angle, we must make sure that $\left|\frac{{\bf v}\cdot {\bf w}}{||{\bf v}||\, ||{\bf w}||}\right|\leq 1$ .

Cauchy-Schwarz Inequality

This last inequality is indeed true for $n$ -dimensional vectors in high-dimensional linear algebra.

In fact, it is important enough to have a name. It is called the Cauchy-Schwarz inequality.

Theorem 1.7.3 (Cauchy-Schwarz inequality): Let ${\bf v},{\bf w}\in {\Bbb R}^{n}$ . Then $|{\bf v}\cdot {\bf w}|\leq ||{\bf v}||\, ||{\bf w}||$ . In terms of their components $v_{1},v_{2},\ldots, v_{n}$ and $w_{1},w_{2},\ldots,w_{n}$ , this is equivalent to $\left(\displaystyle\sum_{i=1}^{n}v_{i}w_{i}\right)^{2}\leq \left(\displaystyle\sum_{i=1}^{n}v_{i}^{2}\right)\left(\displaystyle\sum_{i=1}^{n}w_{i}^{2}\right)$ .

The proof of this is quite tricky. I made a video where I gave the idea of the proof. Your teacher may have you do work to make this into a true proof.

Idea of the proof of the Cauchy-Schwarz Inequality

It is still an open question whether it is a good idea to define the angle between two vectors in high-dimensional linear algebra in this way.

Suffice it to say that it is a good idea. One thing this justifies is our drawing of the right angle when we visualized the least-squares solution as it related to five-dimensional vectors above. This picture emphasizes that, even in five-dimensional space, the shortest distance between a point and a plane is along a line segment perpendicular to the plane.

Linear Transformations and Matrices

Let $m$ and $n$ be positive integers. If $T:{\Bbb R}^{n}\longrightarrow {\Bbb R}^{m}$ is a linear transformation, then there will be an $m\times n$ matrix $A$ that will define $T$ via matrix multiplication of $A$ times a vector ${\bf x}\in {\Bbb R}^{n}$ . Conversely, any matrix multiplication like this defines a linear transformation.

The definition of a linear transformation in this context still has the same form as before. A function $T:{\Bbb R}^{n}\longrightarrow {\Bbb R}^{m}$ is a linear transformation if $T(s{\bf u}+t{\bf v})=sT({\bf u})+tT({\bf v})$ for all $s,t\in {\Bbb R}$ and for all ${\bf u},{\bf v}\in {\Bbb R}^{n}$ .

Suppose there are constants $a_{ij}$ , for $i=1,2,\ldots,m$ and $j=1,2,\ldots,n$ , such that the following formula holds true.

$T({\bf x})=T\left(\left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right]\right)=\left[\begin{array}{c} a_{11}x_{1}+a_{12}x_{2}+\cdots +a_{1n}x_{n} \\ a_{21}x_{1}+a_{22}x_{2}+\cdots +a_{2n}x_{n} \\ \vdots \\ a_{m1}x_{1}+a_{m2}x_{2}+\cdots +a_{mn}x_{n}\end{array}\right]$

Then

$T({\bf x})=T\left(\left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right]\right)=x_{1}\left[\begin{array}{c} a_{11} \\ a_{21} \\ \vdots \\ a_{m1} \end{array} \right]+x_{2}\left[\begin{array}{c} a_{12} \\ a_{22} \\ \vdots \\ a_{m2} \end{array} \right]+\cdots + x_{n}\left[\begin{array}{c} a_{1n} \\ a_{2n} \\ \vdots \\ a_{mn} \end{array} \right]$

This is a linear combination of $n$ ( $m$ -dimensional) vectors with corresponding weights $x_{1},x_{2},\ldots,x_{n}$ . If we create an $m\times n$ matrix $A$ with the various $a_{ij}$ as its entries, then this is what the product $A{\bf x}$ means.

Symbolically,

$T({\bf x})=A{\bf x}=\left[\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array}\right]\left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right]$ $=x_{1}\left[\begin{array}{c} a_{11} \\ a_{21} \\ \vdots \\ a_{m1} \end{array} \right]+x_{2}\left[\begin{array}{c} a_{12} \\ a_{22} \\ \vdots \\ a_{m2} \end{array} \right]+\cdots +x_{n}\left[\begin{array}{c} a_{1n} \\ a_{2n} \\ \vdots \\ a_{mn} \end{array} \right]$

Another way to think of this is as follows. Let ${\bf a}_{1}=\left[\begin{array}{c} a_{11} \\ a_{21} \\ \vdots \\ a_{m1} \end{array} \right], {\bf a}_{2}=\left[\begin{array}{c} a_{12} \\ a_{22} \\ \vdots \\ a_{m2} \end{array} \right],\ldots, {\bf a}_{n}=\left[\begin{array}{c} a_{1n} \\ a_{2n} \\ \vdots \\ a_{mn} \end{array} \right]$ be the columns of $A$ . In fact, we will even write $A=\left[{\bf a}_{1}\ {\bf a}_{2}\ \cdots {\bf a}_{n}\right]$ . Then $A{\bf x}=\left[{\bf a}_{1}\ {\bf a}_{2}\ \cdots {\bf a}_{n}\right]{\bf x}=x_{1}{\bf a}_{1}+x_{2}{\bf a}_{2}+\cdots+x_{n}{\bf a}_{n}=\displaystyle\sum_{i=1}^{n}x_{i}{\bf a}_{i}$ .

When Will $T$ Be Onto? When Will It Be One-to-One?

Under what conditions will a linear transformation $T:{\Bbb R}^{n}\longrightarrow {\Bbb R}^{m}$ with matrix representative $A$ be onto and/or one-to-one?

We will explore this more deeply in Chapter 2 of Visual Linear Algebra Online. At the moment, we just make a few intuitive “probabilistic” statements. Think of these statements as reflecting what happens when we choose the entries of $A$ at random.

These statements are related to the dimensions of the domain and codomain. They are also related to the fact that linear transformations are relatively “simple”. Nothing too strange happens when we look at the mapping properties of linear transformations.

If $n>m$ , then $T$ maps a higher-dimensional space to a lower-dimensional space. It has a “collapsing” nature to it. It is most definitely not one-to-one. On the other hand, it is likely to be onto, though this is not guaranteed.

If $n<m$ , then $T$ maps a lower-dimensional space to a higher-dimensional space. It is most definitely not onto. On the other hand, it is likely to be one-to-one, though this is not guaranteed.

Finally, if $n=m$ , then the domain and codomain of $T$ have the same dimension. It turns out that $T$ is likely to be both one-to-one and onto in this situation, though neither property is guaranteed. However, it does turn out that these two properties are actually equivalent in this situation. This should be somewhat surprising! They are certainly not equivalent for general functions. There must be something special about linear transformations!

Row Operations and Reduced Row Echelon Form

For any particular example, the question of whether the mapping is one-to-one and/or onto can be answered using elementary row operations.

Let’s start by considering the line of best fit example from above. Recall that the formula for $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{5}$ is

To confirm that $T$ is not onto, it suffices to find just one vector in five-dimensional space that is not in the image $T({\Bbb R}^{2})$ . Practically any vector in ${\Bbb R}^{5}$ will do, including our vector from the right-hand side of the original overdetermined system ${\bf v}=\left[\begin{array}{c} 4 \\ 3 \\ 3 \\ 2 \\ 0 \end{array}\right]$ .

Elementary Row Operations on the Augmented Matrix

Elementary row operations on the augmented matrix are shown below.

$\left[\begin{array}{ccc} 1 & 1 & 4 \\ 2 & 1 & 3 \\ 3 & 1 & 3 \\ 4 & 1 & 2 \\ 5 & 1 & 0 \end{array}\right]\xrightarrow{\begin{array}{c} -2R_{1}+R_{2}\rightarrow R_{2} \\ -3R_{1}+R_{3}\rightarrow R_{3} \\ -4R_{1}+R_{4}\rightarrow R_{4} \\ -5R_{1}+R_{5}\rightarrow R_{5} \end{array}}\left[\begin{array}{ccc} 1 & 1 & 4 \\ 0 & -1 & -5 \\ 0 & -2 & -9 \\ 0 & -3 & -14 \\ 0 & -4 & -20 \end{array}\right]\xrightarrow{-R_{2}\rightarrow R_{2}}\left[\begin{array}{ccc} 1 & 1 & 4 \\ 0 & 1 & 5 \\ 0 & -2 & -9 \\ 0 & -3 & -14 \\ 0 & -4 & -20 \end{array}\right]$

$\left[\begin{array}{ccc} 1 & 1 & 4 \\ 0 & 1 & 5 \\ 0 & -2 & -9 \\ 0 & -3 & -14 \\ 0 & -4 & -20 \end{array}\right]\xrightarrow{\begin{array}{c} 2R_{2}+R_{3}\rightarrow R_{3} \\ 3R_{2}+R_{4}\rightarrow R_{4} \\ 4R_{2}+R_{5}\rightarrow R_{5} \end{array}}\left[\begin{array}{ccc} 1 & 1 & 4 \\ 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array}\right]$

This is enough to confirm that ${\bf v}\not\in \mbox{Im}(T)=\mbox{Col}(A)$ . The reason is because the third and fourth rows of the last matrix are equivalent to the statements $0=1$ . This is a false statement and therefore a contradiction to the assumption that there is a solution. The original system is indeed inconsistent and $T$ is not onto.

Continued Reduction to Reduced Row Echelon Form (RREF)

Though it is not required to confirm that $T$ is not onto, let us continue “reducing” this matrix with row operations. This will provide practice with row operations towards the ultimate goal of seeing the reduced row echelon form (RREF) of the matrix.

The first four rows of the final matrix above have leading entries (they are also “leading ones”). These are the leftmost nonzero entries of those rows. To continue the process toward reduced row echelon form, we need to make sure the leading entry in each row is to the right of the leading entry of the row above it.

This is not true for the leading entry of the fourth row. Therefore, we “eliminate” it by a replacement elementary row operation.

$\left[\begin{array}{ccc} 1 & 1 & 4 \\ 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array}\right]\xrightarrow{-R_{3}+R_{4}\rightarrow R_{4}}\left[\begin{array}{ccc} 1 & 1 & 4 \\ 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]$

This new matrix now satisfies the condition that the leading entry in each row is to the right of the leading entry of the row above it. This matrix is now in row echelon form (REF).

To proceed to reduced row echelon form (RREF), we now do replacement operations to eliminate the entries above the leading ones, moving from right to left. Here are the steps.

$\left[\begin{array}{ccc} 1 & 1 & 4 \\ 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]\xrightarrow{\begin{array}{c}-5R_{3}+R_{2}\rightarrow R_{2} \\ -4R_{3}+R_{1}\rightarrow R_{1} \end{array}}\left[\begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]\xrightarrow{-R_{2}+R_{1}\rightarrow R_{1}}\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]$

Because this corresponds to an augmented matrix for the original system involving two variables $m$ and $b$ , the resulting equivalent system is

$\begin{cases}\begin{array}{c}m=0 \\ b=0 \\ 0 = 1 \end{array} \end{cases}$

As we saw before, the last of these equations is a contradiction to the assumption that there is a solution. Therefore, there is no solution. The system is inconsistent (and no, $m$ and $b$ are not both zero).

Description of Reduced Row Echelon Form (RREF)

Here are descriptions of both row echelon form (REF) and reduced row echelon form. These apply to any matrix, augmented or not.

Definition 1.7.1: A matrix is in row echelon form (REF) if

All nonzero rows (rows with at least one nonzero entry) are above any rows of all zeros.
Each leading entry of a row is in a column to the right of the leading entry of the row above it. Therefore, all entries in a column below a leading entry are zeros.

Definition 1.7.2: A matrix is in reduced row echelon form (RREF) if conditions (1) and (2) from Definition 1.7.1 hold, and if

The leading entry in each nonzero row is 1.
Each leading 1 is the only nonzero entry in its column.

A matrix is equivalent to exactly one RREF form obtained from row operations. This is a theorem, but we will not prove it.

Theorem 1.7.3: Every matrix is row equivalent to a unique RREF matrix.

Is T one-to-one? Determining the Kernel (Null Space) is Sufficient to Decide

To show that $T$ is one-to-one, we must prove that $T({\bf x})=T({\bf y})$ implies that ${\bf x}={\bf y}$ .

Certainly if $T$ is one-to-one, the kernel of $T$ (null space of its matrix $A$ ) will be just the zero vector ${\bf 0}$ (as an element of the domain). By definition, $T({\bf 0})=A{\bf 0}=0{\bf a}_{1}+0{\bf a}_{2}+\cdots +0{\bf a}_{n}={\bf 0}$ . But the fact that $T$ is one-to-one implies nothing else can get mapped to the zero vector in the codomain.

What is more surprising is the following fact, which we prove using the definition of linearity found in Section 1.4, “Linear Transformations in Two Dimensions”. The proof is quite short once you see the trick.

Theorem 1.7.4: Let $T:{\Bbb R}^{n}\longrightarrow {\Bbb R}^{m}$ be a linear transformation. If $\mbox{Ker}(T)=\{{\bf 0}\}\subseteq {\Bbb R}^{n}$ , then $T$ is one-to-one.

Proof:

Suppose $T({\bf x})=T({\bf y})$ . Then $T({\bf x})-T({\bf y})={\bf 0}$ . But $T$ is a linear transformation. Therefore, $T({\bf x}-{\bf y})=T({\bf x})-T({\bf y})={\bf 0}$ . Now the fact that $T$ is one-to-one allows us to conclude that ${\bf x}-{\bf y}={\bf 0}$ . Therefore, ${\bf x}={\bf y}$ .

Q.E.D.

Combining Theorem 1.7.4 with the discussion two paragraphs above it gives the following biconditional (if and only if) theorem.

Theorem 1.7.5: Let $T:{\Bbb R}^{n}\longrightarrow {\Bbb R}^{m}$ be a linear transformation. Then $\mbox{Ker}(T)=\{{\bf 0}\}\subseteq {\Bbb R}^{n}$ if and only if $T$ is one-to-one.

Row Operations on the Corresponding Homogeneous System

Now consider the homogeneous system corresponding to the data-fitting example linear transformation from above.

$\begin{cases}\begin{array}{c} m+b=0 \\ 2m+b=0 \\ 3m+b=0 \\ 4m+b=0 \\ 5m+b=0 \end{array} \end{cases}$

The corresponding augmented matrix and resulting row operations begin as follows.

$\left[\begin{array}{ccc} 1 & 1 & 0 \\ 2 & 1 & 0 \\ 3 & 1 & 0 \\ 4 & 1 & 0 \\ 5 & 1 & 0 \end{array}\right]\xrightarrow{\begin{array}{c} -2R_{1}+R_{2}\rightarrow R_{2} \\ -3R_{1}+R_{3}\rightarrow R_{3} \\ -4R_{1}+R_{4}\rightarrow R_{4} \\ -5R_{1}+R_{5}\rightarrow R_{5} \end{array}}\left[\begin{array}{ccc} 1 & 1 & 0 \\ 0 & -1 & 0 \\ 0 & -2 & 0 \\ 0 & -3 & 0 \\ 0 & -4 & 0 \end{array}\right]\xrightarrow{-R_{2}\rightarrow R_{2}}\left[\begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & -2 & 0 \\ 0 & -3 & 0 \\ 0 & -4 & 0 \end{array}\right]$

This quickly leads to the unique equivalent RREF matrix.

$\left[\begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 5 \\ 0 & -2 & 0 \\ 0 & -3 & 0 \\ 0 & -4 & 0 \end{array}\right]\xrightarrow{\begin{array}{c} 2R_{2}+R_{3}\rightarrow R_{3} \\ 3R_{2}+R_{4}\rightarrow R_{4} \\ 4R_{2}+R_{5}\rightarrow R_{5} \end{array}}\left[\begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]\xrightarrow{-R_{2}+R_{1}\rightarrow R_{1}}\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]$

The top two rows of this matrix correspond to the equations $m=0$ and $b=0$ . Furthermore, there is no contradiction that occurs. The homogeneous system has a unique solution. The kernel (null space) has just one element $\mbox{Ker}(T)=\mbox{Nul}(A)=\{{\bf 0}\}=\left\{\left[\begin{array}{c} 0 \\ 0 \end{array}\right]\right\}$ .

By Theorem 1.7.4, this implies that $T$ is one-to-one.

Another Example

Let’s consider a second example in high-dimensional linear algebra where the matrix of the linear transformation is the transpose of the preceding example, where we swap the rows and columns. This has nothing to do with the original data-fitting problem.

Define $T:{\Bbb R}^{5}\longrightarrow {\Bbb R}^{2}$ by the formula

$T({\bf x})=A{\bf x}=\left[\begin{array}{ccccc} 1 & 2 & 3 & 4 & 5 \\ 1 & 1 & 1 & 1 & 1 \end{array}\right]\left[\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \\ x_{5} \end{array}\right]$ $x_{1}\left[\begin{array}{c} 1 \\ 1 \end{array}\right]+x_{2}\left[\begin{array}{c} 2 \\ 1 \end{array}\right]+x_{3}\left[\begin{array}{c} 3 \\ 1 \end{array}\right]+x_{4}\left[\begin{array}{c} 4 \\ 1 \end{array}\right]+x_{5}\left[\begin{array}{c} 5 \\ 1 \end{array}\right]$

Of course, this gives

$T({\bf x})=A{\bf x}=\left[\begin{array}{c} x_{1}+2x_{2}+3x_{3}+4x_{4}+5x_{5} \\ x_{1}+x_{2}+x_{3}+x_{4}+x_{5}\end{array}\right]$

T is not one-to-one

Such a function is definitely not one-to-one. By Theorem 1.7.5, this can be confirmed by computing the kernel (null space) and seeing that it contains nonzero vectors. Here are elementary row operations on the augmented matrix for the corresponding homogeneous system, with a last column of zeros, to RREF.

$\left[\begin{array}{cccccc} 1 & 2 & 3 & 4 & 5 & 0 \\ 1 & 1 & 1 & 1 & 1 & 0 \end{array}\right]\xrightarrow{R_{1}\leftrightarrow R_{2}}\left[\begin{array}{cccccc} 1 & 1 & 1 & 1 & 1 & 0 \\ 1 & 2 & 3 & 4 & 5 & 0 \end{array}\right]$

Next,

$\left[\begin{array}{cccccc} 1 & 1 & 1 & 1 & 1 & 0 \\ 1 & 2 & 3 & 4 & 5 & 0 \end{array}\right]\xrightarrow{-R_{1}+R_{2}\rightarrow R_{2}}\left[\begin{array}{cccccc} 1 & 1 & 1 & 1 & 1 & 0 \\ 0 & 1 & 2 & 3 & 4 & 0 \end{array}\right]$

Finally,

$\left[\begin{array}{cccccc} 1 & 1 & 1 & 1 & 1 & 0 \\ 0 & 1 & 2 & 3 & 4 & 0 \end{array}\right]\xrightarrow{-R_{2}+R_{1}\rightarrow R_{1}}\left[\begin{array}{cccccc} 1 & 0 & -1 & -2 & -3 & 0 \\ 0 & 1 & 2 & 3 & 4 & 0 \end{array}\right]$

This is a matrix in RREF form (check the conditions described above). It corresponds to the following system, which is equivalent to the original homogeneous system.

$\begin{cases} \begin{array}{ccccccccccc} x_{1} & & & - & x_{3} & - & 2x_{4} & - & 3x_{5} & = & 0 \\ & & x_{2} & + & 2x_{3} & + & 3x_{4} & + & 4x_{5} & = & 0 \end{array} \end{cases}$

From this, we see that $x_{3}$ , $x_{4}$ , and $x_{5}$ are free variables, while $x_{1}$ and $x_{2}$ are basic. We can therefore describe the kernel of $T$ in parametric vector form as follows.

$\mbox{Ker}(T)=\mbox{Nul}(A)=\left\{x_{3}\left[\begin{array}{c} 1 \\ -2 \\ 1 \\ 0 \\ 0 \end{array}\right]+x_{4}\left[\begin{array}{c} 2 \\ -3 \\ 0 \\ 1 \\ 0 \end{array}\right]+x_{5}\left[\begin{array}{c} 3 \\ -4 \\ 0 \\ 0 \\ 1 \end{array}\right]\, \biggr|\, x_{3},x_{4},x_{5}\in {\Bbb R}\right\}$

As we will see in Chapter 2, the three vectors $\left[\begin{array}{c} 1 \\ -2 \\ 1 \\ 0 \\ 0 \end{array}\right]$ , $\left[\begin{array}{c} 2 \\ -3 \\ 0 \\ 1 \\ 0 \end{array}\right]$ , and $\left[\begin{array}{c} 3 \\ -4 \\ 0 \\ 0 \\ 1 \end{array}\right]$ in ${\Bbb R}^{5}$ are “linearly independent“. These three vectors will not all be in the same two-dimensional plane in ${\Bbb R}^{5}$ .

Instead, this means that $\mbox{Ker}(T)=\mbox{Nul}(A)$ is a three-dimensional “plane” through the origin in five-dimensional space.

And, as already mentioned, this is enough to conclude that $T$ is not one-to-one.

As an interesting aside, note that, by using the dot product, you can check that these three vectors are also perpendicular to the columns of first example:

$\left[\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ 5 \end{array}\right]\mbox{ and } \left[\begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{array}\right]$

This is one instance of a general theorem relating the column space of a matrix with the null space of its transpose.

T is onto

It is likely that $T$ is onto. In other words, the image $T({\Bbb R}^{5})$ is all of ${\Bbb R}^{2}$ .

How can this be confirmed? By showing that an arbitrary non-homogeneous (inhomogeneous) system can be solved.

$\begin{cases} \begin{array}{ccccccccccc} x_{1} & + & 2x_{2} & + & 3x_{3} & + & 4x_{4} & + & 5x_{5} & = & a \\ x_{1} & + & x_{2} & + & x_{3} & + & x_{4} & + & x_{5} & = & b \end{array} \end{cases}$

Below are the row operations to RREF. Notice that they are the same row operations as we did above for the homogeneous system. First,

$\left[\begin{array}{cccccc} 1 & 2 & 3 & 4 & 5 & a \\ 1 & 1 & 1 & 1 & 1 & b \end{array}\right]\xrightarrow{R_{1}\leftrightarrow R_{2}}\left[\begin{array}{cccccc} 1 & 1 & 1 & 1 & 1 & b \\ 1 & 2 & 3 & 4 & 5 & a \end{array}\right]$

Next,

$\left[\begin{array}{cccccc} 1 & 1 & 1 & 1 & 1 & b \\ 1 & 2 & 3 & 4 & 5 & a \end{array}\right]\xrightarrow{-R_{1}+R_{2}\rightarrow R_{2}}\left[\begin{array}{cccccc} 1 & 1 & 1 & 1 & 1 & b \\ 0 & 1 & 2 & 3 & 4 & a-b \end{array}\right]$

Finally,

$\left[\begin{array}{cccccc} 1 & 1 & 1 & 1 & 1 & b \\ 0 & 1 & 2 & 3 & 4 & a-b \end{array}\right]\xrightarrow{-R_{2}+R_{1}\rightarrow R_{1}}\left[\begin{array}{cccccc} 1 & 0 & -1 & -2 & -3 & -a+2b \\ 0 & 1 & 2 & 3 & 4 & a-b \end{array}\right]$

This is a matrix in RREF form. It corresponds to the following system, which is equivalent to the original inhomogeneous system.

$\begin{cases} \begin{array}{ccccccccccc} x_{1} & & & - & x_{3} & - & 2x_{4} & - & 3x_{5} & = & -a+2b \\ & & x_{2} & + & 2x_{3} & + & 3x_{4} & + & 4x_{5} & = & a-b \end{array} \end{cases}$

This shows that there are indeed solutions to the arbitrary inhomogeneous system so that $T$ is onto.

In fact, for fixed $a$ and $b$ , the parametric vector form of the solution set is just a “translation” of the three-dimensional kernel of $T$ inside five-dimensional space. This set no longer goes through the origin unless $a=b=0$ , but it is “parallel” to the kernel. This is no accident.

$\left\{\left[\begin{array}{c} -a+2b \\ a-b \\ 0 \\ 0 \\ 0 \end{array}\right]+x_{3}\left[\begin{array}{c} 1 \\ -2 \\ 1 \\ 0 \\ 0 \end{array}\right]+x_{4}\left[\begin{array}{c} 2 \\ -3 \\ 0 \\ 1 \\ 0 \end{array}\right]+x_{5}\left[\begin{array}{c} 3 \\ -4 \\ 0 \\ 0 \\ 1 \end{array}\right]\, \biggr|\, x_{3},x_{4},x_{5}\in {\Bbb R}\right\}$

Summarizing the Examples in Relation to the Rank-Nullity Theorem

In our first, data-fitting related linear transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{5}$ with $5\times 2$ matrix

$A=\left[\begin{array}{cc} 1 & 1 \\ 2 & 1 \\ 3 & 1 \\ 4 & 1 \\ 5 & 1 \end{array}\right]$ ,

we saw that the kernel (null space) was “trivial” $\{{\bf 0}\}$ (which is zero-dimensional) and the image was two-dimensional. Note that $0+2=2$ , which is the dimension of the domain of $T$ , as well as the number of columns of $A$ .

In the second example, the linear transformation $T:{\Bbb R}^{5}\longrightarrow {\Bbb R}^{2}$ had $2\times 5$ matrix

$A=\left[\begin{array}{ccccc} 1 & 2 & 3 & 4 & 5 \\ 1 & 1 & 1 & 1 & 1 \end{array}\right]$ .

Here we got a three-dimensional kernel and a two-dimensional image. The sum $3+2=5$ is the dimension of the domain of $T$ , as well as the number of columns of $A$ .

These facts are not coincidences. The Rank-Nullity Theorem (or just “Rank Theorem”) guarantees this will always be true.

Theorem 1.7.6 (Rank-Nullity Theorem): Suppose $T:{\Bbb R}^{n}\longrightarrow {\Bbb R}^{m}$ is a linear transformation with (standard) $m\times n$ matrix representative $A$ . Then the dimension of the kernel of $T$ (null space of $A$ ) plus the dimension of the image of $T$ (column space of $A$ ) equals $n$ , the dimension of the domain of $T$ (the number of columns of $A$ ).

Exercises in High-Dimensional Linear Algebra

Let ${\bf x}=\left[\begin{array}{c} 4 \\ -3 \\ 7 \\ 2 \end{array}\right]$ and ${\bf y}=\left[\begin{array}{c} -1 \\ 5 \\ 6 \\ -4 \end{array}\right]$ . (a) Find $7{\bf x}+4{\bf y}$ . (b) Find the angle $\theta$ between ${\bf x}$ and ${\bf y}$ with $0\leq \theta\leq \pi=180^{\circ}$ . Approximate your answer to the nearest tenth of a degree.
(a) Use row operations to RREF on the augmented matrix for the following system to solve it. Write your answer in parametric vector form: $\begin{cases} \begin{array}{ccccccccc} x_{1} & - & 3x_{2} & + & 2x_{3} & + & 7x_{4} & = & -3 \\ 2x_{1} & + & 3x_{2} & - & 5x_{3} & + & 7x_{4} & = & 4 \end{array}\end{cases}$ . (b) Describe the kernel and image of the corresponding linear transformation $T$ . (c) Decide whether $T$ is one-to-one and/or onto. Defend your answers.
Consider the data set $(1,-1), (2,2), (3,4), (4,5), (5,7)$ . The (least squares) line of best fit turns out have formula $y=f(x)=1.9x-2.3$ . (a) Graph these points and this line as accurately as you can. (b) Find the sum of the squares of the errors in using this line to estimate the $y$ -coordinates of the data points based on their $x$ -coordinates. (c) If you assume that $y=f(x)=mx+b$ goes through the data points exactly, write down the corresponding system of five equations and two unknowns that would be satisfied. (d) Do row operations with the corresponding augmented matrix for the system in (c) to confirm that the system has no solution. (e) Describe the kernel and image of the linear transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{5}$ defined by the left-hand sides of the system of equations from part (c). (f) Compute the distance $||T({\bf x})-{\bf v}||$ in ${\Bbb R}^{5}$ that is minimized when ${\bf x}=\left[\begin{array}{c} m \\ b \end{array}\right]=\left[\begin{array}{c} 1.9 \\ -2.3 \end{array}\right]$ and ${\bf v}$ is the five-dimensional vector from the right-hand sides of the equations in part (c).
Prove Theorem 1.7.1.
Prove Theorem 1.7.2.
A homogeneous system of three linear equations and five unknowns is solved using elementary row operations. It is found that there are three free variables that result in a kernel that is three-dimensional. Will the linear transformation corresponding to this system be an onto function? Explain why or why not.

Video for Section 1.7

Here is a video overview of the content of this section.