The Big Ideas of Calculus - Infinity is Really Big

Calculus 1, Lecture 1

The area of a circle can be found with the Infinity Principle. This is described by Steven Strogatz in his book Infinite Powers.

Calculus is often described as the mathematics of change. In terms of a short description, this is apt.

You might even say this description gives us a view of the big ideas of calculus, without really getting into any details.

But what does it mean? The only way to find out is by getting into the details.

Here at Infinity is Really Big, this is the first of many posts where I (Bill Kinney) will get into some of the details. However, if you want even more details, you will want to be sure to watch the corresponding lectures I gave at Bethel University in St. Paul, MN during the fall semester of 2019.

Here is the entire first lecture.

Calculus 1, Lecture 1: The Big Ideas of Calculus (Rates & Areas, the Infinity Principle and Circular Area)

Lecture Summary and Main Points of the Big Ideas of Calculus

In lecture 1, I start by emphasizing the beauty of calculus through both the eyes of faith and science. I am a Christian, and my purpose in life is to glorify God and enjoy Him forever. Seeing how mathematics reflects reality is part of this. Using mathematics to help others is part of this purpose as well. I am so thankful that God has given humans minds to understand many things, including Him.

Part of humankind’s quest to understand God is reflected in our desire to understand creation. Ancient people were inspired, for example, to understand the motion of bodies (masses) in “the heavens” (outer space). The subject even has a name: celestial mechanics. This is also a subject of great interest to me and many others in modern times.

Kepler’s Laws are an empirical description of how the planets move around the sun. Ultimately, Isaac Newton was inspired to “discover” or “create” calculus as a way to explain Kepler’s laws from more general laws. These were the Laws of Motion as well as the Law of Universal Gravitation. The second of these laws is the really astonishing one. It’s amazing to think that every mass in the universe attracts every other mass in the universe!

Visual Examples

At that point in the lecture I go on to describing a bunch of visual examples. These example illustrate the close connection between rates of change (derivatives) and areas (integrals). These are considered initially in the easiest case: when the rates are constant. The examples include: 1) the motion of cars, 2) fluid flow into tanks, 3) bacterial population growth.

The key principles in these examples are these: 1) when the rate of change (derivative) is constant, the total accumulated value (distance, volume, or population) can be found by multiplication. Also, 2) the product can then be visualized as the area of a rectangle under the graph of the constant derivative.

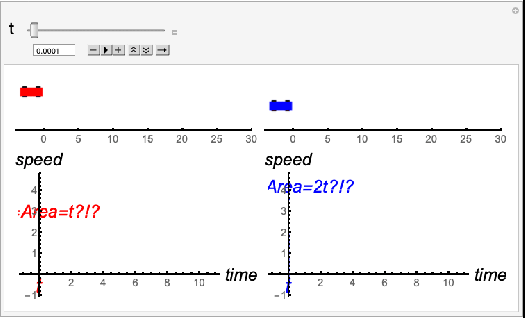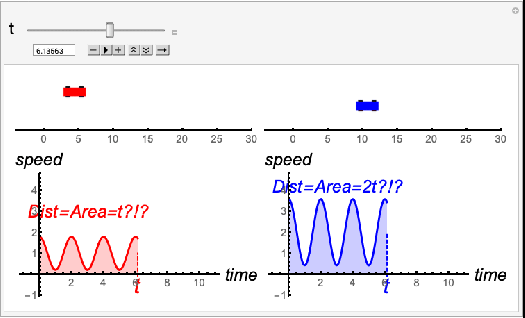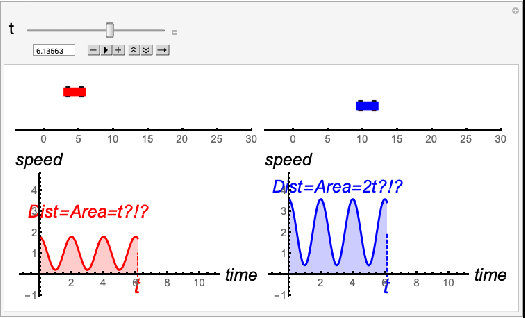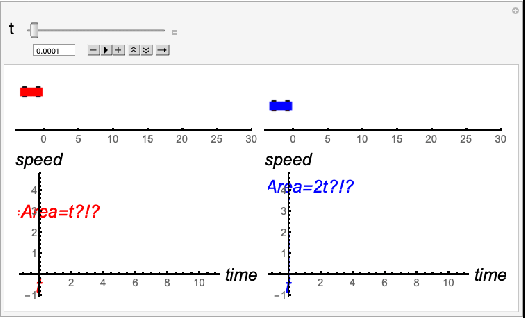
But what if the rate of change is not constant? That’s where “true” calculus is needed. The area under the graph of the derivative is still the accumulated value we desire. But the formula for that area is no longer simple to find. We will need to develop techniques to compute, or at least approximate, these areas.

The following animation shows a situation where the derivative is not constant. The speed of the cars increases and decreases as they move. Finding the distance traveled in this situation, based on the speed, is difficult. It is a challenge that calculus seeks to conquer.

Motion at a non-constant speed is related to the big ideas of calculus. — Two cars moving at a non-constant speed. The areas still equal the distance traveled for each car. However, the formula for the distance traveled is not simple. The areas do **NOT**, in fact, equal $t$ and $2t$ .

Two cars moving at a non-constant speed. The areas still equal the distance traveled for each car. However, the formula for the distance traveled is not simple. The areas do **NOT**, in fact, equal $t$ and $2t$ .

The Area of a Circle

Have you ever wondered why the formula for the area of a circle involves $\pi$ ? Saying “well, it’s a circle” is not a good enough answer.

The definition of $\pi$ is the ratio of the circumference of any circle to its diameter. This gives the formula $C=\pi D=2\pi r$ . But why should $\pi$ be also involved in the area formula: $A=\pi r^{2}$ ?

The intuition behind this result is expressed in an elegant way by Steven Strogatz in both his book Infinite Powers and the talk below “The Beauty of Calculus”. They are based the principle he has named “The Infinity Principle”. This is definitely part of the big ideas of calculus.

“The Beauty of Calculus,’ a Lecture by Steven Strogatz

Quoting page xvi of Infinite Powers, the Infinity Principle says this.

To shed light on any continuous shape, object, motion, process, or phenomenon – no matter how wild and complicated it may appear – reimagine it as an infinite series of simpler parts, analyze those, and then add the results back together to make sense of the original whole.
Page xvi of Infinite Powers

You can also see this used in the following video by Grant Sanderson at the 3Blue1Brown channel. It is part of his “The Essence of Calculus” series.

The Essence of Calculus, Chapter 1

A Couple Animations from My Lecture

In my lecture, I ended by illustrating the ideas in Infinite Powers and these videos with animations made with the Computer-Algebra System (CAS) Mathematica, by Wolfram Research. The first animation is based on “Infinite Powers”.

In the limit as the number of slices of the ‘pie’ goes to infinity, we see that the area of the circle must be the area of the limiting rectangle.

The second animation is based on “The Essence of Calculus”.

*In the limit as the number of rings of the ‘pie’ goes to infinity, we see that the area of the circle must be the area of the limiting triangle.*

In spite of all the formulas in calculus, these big ideas get at the heart of what calculus is truly about. I hope you enjoy my lectures and these other resources as well!