Calculus 2, Lectures 5A through 6 (Videotaped Fall 2016)

The Fundamental Theorem of Calculus is often split into two forms in textbooks.
These forms are typically called the “First Fundamental Theorem of Calculus” and the “Second Fundamental Theorem of Calculus”, but they are essentially two sides of the same coin, which we can just call the “Fundamental Theorem of Calculus”, or even just “FTC”, for short.
In my current series of blog posts based on my Calculus 2 lectures at Bethel University from the Fall 2016 semester, I have already been making use of the FTC. This is natural to do for a second semester calculus course, because the FTC is usually introduced in the first semester.
In my second post, “Integration by Substitution (Method of Integration)”, I discuss how the FTC is relevant to the substitution method. The key definite integral equation that is derived there, assuming we have appropriately nice functions and
, is
. The FTC along with the Chain Rule are the facts that are necessary to prove this.
On the other hand, in my third post, “Integration by Parts (and Linear Motion)”, it is the Product Rule that must be combined with the FTC to obtain the key equation. This is equation is typically written as , where
and
are suitably nice functions. The notation
is understood to mean
, just as
means
.
But what is the FTC (both parts)? And why is it true? Let’s explore!
The First Fundamental Theorem of Calculus
If you ask a studious calculus student what the Fundamental Theorem of Calculus is, what will they answer? In all likelihood, that student will tell you that it gives a method to evaluate definite integrals.
For a function whose graph is always above the horizontal axis, it therefore gives you a way to find the area under its graph and above the axis.
Example 1: Find an Area under the Graph of the Squaring Function using the FTC
For example, consider the definite integral . This symbol represents the area of the region
shown below. The region
is bounded by the graph of
, the
-axis, and the vertical lines
and
.

How is this done? The FTC tells us to find an antiderivative of the integrand function and then compute an appropriate difference.
An antiderivative of is
. Since the limits of integration in
are
and
, the FTC tells us that we must compute
. The answer is
.
We have indeed used the FTC here. But which version?
The version we just used is typically called the First Fundamental Theorem of Calculus. But what is its precise statement?
Statement of the First Fundamental Theorem of Calculus
Here is one way to state the 1st FTC.
First Fundamental Theorem of Calculus: Suppose that the function 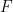 is an antiderivative of the function
is an antiderivative of the function  on an interval
on an interval ![[a,b] [a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0) , so that
, so that 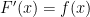 for all
for all  in
in ![[a,b] [a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0) , then
, then 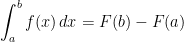 .
.
This is a pretty amazing theorem. It tells us that finding an antiderivative is most of the way to finding what could be, quite possibly, a very complicated area.
This is a vast (infinite) extension of what you learned about areas of objects in geometry!
On the other hand, there is no guarantee that an antiderivative will be easy or even possible to find.
Example 2: Find a Complicated Area with the First FTC
For instance, consider the definite integral . You should check, using the Product Rule and Chain Rule, that
is an antiderivative of the integrand
.
Therefore, by the FTC, we compute
This is indeed the area of the complicated region shown in the figure below.

Signed Area Interpretation and Computation
More broadly, definite integrals are defined to give what are sometimes called “signed” areas rather than “true” areas.
If for all
in a closed interval
, then
certainly represents a true area. It is the area under the graph of
, above the
axis, and between the vertical lines at
and
.
But if the graph of goes below the
axis, then
represents something different. It represents the area “under the graph” when it is above the axis minus the area “above the graph” when it is below the axis.
This will be more clear if we consider and example with a graph.
Example 3: Find a Signed Area with the First FTC
Let . Then the function
defined by
is an antiderivative of
(over the whole real number line
). Then, for example, by the 1st FTC,
We see that the answer is negative. In fact, in the picture below, with the (positive) areas labeled ,
, and
, the definite integral above equals
.
In other words, areas that are below the graph when the graph is above the axis contribute positively to the value of the integral, while areas that are above the graph when the graph is below the axis contribute negatively to the integral.

In fact, and
.
On the other hand,
since when
.
Therefore,
The First Fundamental Theorem of Calculus Might Seem Like Magic
When you think about these area and signed area applications, the First Fundamental Theorem of Calculus might seem quite “magical”.
Is there any way to understand it intuitively? Yes, an intuitive (but non-rigorous) approach involving so-called infinitesimals (infinitely small quantities) can be used to gain insight. But we will save that topic for later in this post.
In the next main section, however, we will explore the Second Fundamental Theorem of Calculus. The 2nd FTC is more difficult to understand than the 1st FTC when you first encounter it. However, once the main conceptual ideas about it are understood, it is actually less mysterious. Moreover, the 2nd FTC can actually be used to give a relatively “quick” proof of the 1st FTC.
In Lecture 5A from Fall 2016, I start describing how to gain an understanding the Second Fundamental Theorem of Calculus through examples.
Lecture 5A: the Second Fundamental Theorem of Calculus (and Linear Motion)
I start Lecture 5A by considering a linear motion example with a piecewise linear velocity function.
The piecewise linear velocity function has the formula .
This means the velocity is negative if and positive if
(see the graph in the thumbnail of the video above). If we think of motion to the right as being a positive velocity and motion to the left as being a negative velocity, then the object starts out by moving to the left before turning around at time
and moving to the right thereafter.
Now let . By the signed area interpretation of the definite integral, we can derive the following (see the graph in the thumbnail of the video above):
- If
, then
.
- If
, then
, so
. This simplifies to
.
- And, if
, then
. This also simplifies to
.
Notice that, no matter what is, we have
. We have used the signed area interpretation of the definite integral to “construct” an antiderivative
of the integrand function
!!
This is what the Second Fundamental Theorem of Calculus is all about: integrals (signed areas) define antiderivatives.
Statement of the Second Fundamental Theorem of Calculus
Here is the formal statement of the 2nd FTC. It is sometimes called the Antiderivative Construction Theorem, which is very apt.
Second Fundamental Theorem of Calculus: Suppose that the function  is continuous on the closed interval
is continuous on the closed interval ![[a,b] [a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0) . Define a function
. Define a function 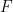 on
on ![[a,b] [a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0) by the formula
by the formula 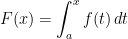 . Then
. Then 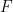 is differentiable on
is differentiable on ![[a,b] [a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0) and
and 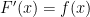 for all
for all  in
in ![[a,b] [a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0) . In other words,
. In other words, 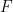 is an antiderivative of
is an antiderivative of  on
on ![[a,b] [a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0) .
.
This can also be written concisely as follows. If is continuous near the number
, then
when
is close to
.
In this equation, it is as if the derivative operator and the integral operator
“undo” each other to leave the original function
.
In fact, this “undoing” property holds with the First Fundamental Theorem of Calculus as well. Its equation can be written as . Or, if you prefer, we can rearrange and use different letters and write the equation from the 1st FTC as
.
Here we see something similar: the integral operator and the derivative operator
“undo” each other to obtain the function
, although we must add on a “constant”
to get equality.
Example 4: An Example to Help You Believe the Second Fundamental Theorem of Calculus
Here is an example to help you believe that the Second Fundamental Theorem of Calculus is true. Suppose is the speed of a moving object, in meters per second, as a function of time
, in seconds. For the sake of illustration, let’s do something a bit strange and let
be our starting time. So our overall time interval is
.
Let be a time with
. What we want to see is that the definite integral
, when thought of as a function of
, is an antiderivative of
.
Since the graph of is the upper half of the unit circle, we can compute the definite integral purely with geometry and trigonometry.
In the graph below, the area of the quarter circle on the left is .
The region on the right can be split into a sector of a circle (a “piece of pie”) and the right triangle shown. By trigonometry, so that
. The area of the sector of the circle is therefore
. Furthermore, the area of the triangle is
.

Putting all this together, we see that .
Now we must check that an antiderivative of
. Use the Product Rule and Chain Rule to confirm this. Here goes:
.
We continue to simplify and get . But this simplifies to
, as desired.
Also note that . In other words, the graph of
also goes through the point
.
The case where can be handled geometrically as well, though you would want to think of it as
, where
would represent an “unshaded” area to the left of the vertical axis. You should get the same simplified formula for
in the end. Give it a try!
This Antiderivative is the Distance Traveled
In fact, the function output represents the distance traveled from time
to time
. Here is an animation that illustrates all this.

Again, the purpose of these examples is to help you believe the truth of the Second Fundamental Theorem of Calculus. Let’s consider another example from the lectures before we explore proofs of the First and Second Fundamental Theorems of Calculus.
Lectures 5B and 6: More Integral Examples
The main content of both Lecture 5B and Lecture 6 is to work through more integral examples. Additionally, in the first 13 minutes of Lecture 5B, I review the Second Fundamental Theorem of Calculus and introduce parametric curves, while the last 8 minutes of Lecture 6 are spent extending the 2nd FTC to a problem that also involves the Chain Rule.
Here is Lecture 5B.
And here is Lecture 6. It is a short lecture because the students took a “mini-exam” that day as well.
In this blog post, we will just focus on the extended problem where the Chain Rule is needed. It’s a pretty “wild” example: buckle up!
Example 5: A Function Defined by an Integral Whose Derivative Must Be Computed with the Chain Rule as well as the 2nd FTC
The problem is to compute the following very complicated-looking derivative:
Before taking this derivative, let’s take the time to graph the integrand function , the appropriate signed area between its graph and the horizontal axis, and the graph of the function
.
Suffice it to say that all this should not be attempted without technology.
The Graph of the Integrand
First, so there is no misunderstanding, we plot on a very “wide” window to show that, while it oscillates like a cosine function, the oscillations do indeed get faster and faster as
increases since
increases faster and faster as
increases.

Now zoom in near , which is the lower limit of integration in the formula for
. The graph of
, as well as the shaded signed area representing the value of
, is shown below. There is a small negative signed area contribution to the integral from
until
that is difficult to see.

The Graph of the Integral
And here now is the graph of very close to
. Note that
. Furthermore, note that
has two local maxima before
. This is consistent with the fact that the
is “accumulating” signed areas for the graph of
above, and that the graph of
above changes sign from positive to negative twice on the interval
. Also note that
. This is the accumulated signed area shown in the graph shown above where
.

When you think about the graph and the formula for , you should realize that the values of
have to be approximated using numerical (approximate) integration. The function
has no simple formula that does not involve an integral sign!!
In spite of this, we can still use the 2nd FTC and the Chain Rule to find a (relatively) simple formula for !!
The Derivative of 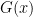
The function is really the composition of two functions. Let
(note the new upper limit of integration) and
. Then
.
By the Chain Rule . But
and, by the Second Fundamental Theorem of Calculus,
.
Therefore,
Isn’t calculus amazing! Who would’ve thunk it?!? Praise God for the details of His creation and His generosity in giving us minds to contemplate and compute such things!
If we graph for
, we should see that it has five zeros on this interval. These correspond to the five critical points of
on this interval in the graph above (where
has local extreme points). The first critical point for the graph of
is so close to the left endpoint that you can’t really see it (it’s “covered” by the big red dot on the left).

Applying these theorems was a lot of fun. But why are the First and Second Fundamental Theorems of Calculus true? We end this blog post by looking at proofs and intuitive justifications.
Proof of the First Fundamental Theorem with the Second Fundamental Theorem
We’ll start by doing something kind of strange. Let’s use the Second Fundamental Theorem of Calculus to prove the First Fundamental Theorem of Calculus. After that, we’ll describe the idea of a proof of the Second Fundamental Theorem of Calculus. Finally, we’ll think about the theorems intuitively using infinitesimals.
Technically speaking, we also need a fact about any two antiderivatives of the same function over an interval: they must be vertical translations of each other (they must “differ by a constant”). This is something that can be proved with the Mean Value Theorem.
Proof of the First Fundamental Theorem of Calculus
Suppose that is an antiderivative of
on the interval
. Let
be defined by
. By the Second Fundamental Theorem of Calculus, we know that
for all
.
Therefore, is an antiderivative of
on
. But this means that there is a constant
such that
for all
.
Now the formula for implies that
. But
. Hence,
.
But as well.
Therefore, and we are done (this also implies that
since variable names don’t matter). Q.E.D.
That was kind of a “slick” proof. Evidently the “hard” work must be involved in proving the Second Fundamental Theorem of Calculus.
We do not give a rigorous proof of the 2nd FTC, but rather the idea of the proof.
Idea of the Proof of the Second Fundamental Theorem of Calculus
Let be continuous on the interval
. Define a function
on
by the formula
(we are implicitly assuming this integral “exists” for all
here).
Our goal is to show that . By the definition of the derivative, we know that
(assuming this limit exists for all
and assuming an appropriate one-sided limit if
or
).
By interval-related properties of integrals (draw a picture of appropriate areas under the graph of to help you understand this), we can write
But if , then
for all
between
and
. Therefore,
. Hence,
when
.
In the limit as , this approximation becomes exact (the continuity of
guarantees this). Therefore,
. Since
was arbitrary, this is true over the entire interval. Q.E.D.
Intuitive Approaches to Understanding These Theorems
Now let’s approach these theorems intuitively. One way to do so is to make use of “infinitely small quantities”, called infinitesimals. Right away, we should give a caveat: in the standard real number system, there are no such things as infinitesimals. They are “convenient fictions” that help to give intuition and to derive formulas in calculus while avoiding limits.
The 1st FTC
Let’s start with the First Fundamental Theorem of Calculus.
Consider an example. Let . Moreover, let’s assume this is a speed, in meters per second, which is the derivative of a distance traveled, in meters. In fact, we can write
, where
is the distance traveled, in meters, from time 0 to time
.
Imagine now that is some specific moment in time. For example, maybe
as shown in the graph below.

Think of The Thin Strip as having an Infinitesimal Area (Infinitesimal Distance Traveled) and Add Up Those Areas By Integrating
In this figure, imagine the shaded thin strip has “infinitesimal” width . In fact, imagine
is so small that this thin strip is actually a rectangle with base
and height
. Its area is then the infinitesimally small product
. This also gives an infinitesimally small distance traveled (since distance equals rate times time for constant rates).
For a given “ending time” , the definite integral
gives the area under this curve between
and
. In fact, the definite integral can be imagined as “adding” all the infinitesimally small products
as
ranges from 0 to
.
But, as already mentioned, these infinitesimally small products are also infinitesimally small distances traveled. When we add them up, we have to get the total distance traveled !
Therefore, . This is the First Fundamental Theorem of Calculus (with
)!
This can take a long time to sink in. Don’t be too upset if you don’t “get it” at first. Keep coming back to it and thinking about it over and over again. It is worth it!
The equation can be summarized this way: to find the total change in a function, you must integrate its rate of change.
The 2nd FTC
We can think about the Second Fundamental Theorem of Calculus with infinitesimals as well.
The key observation is this: the value of determines how “fast” the infinitesimal areas
“accumulate”. Assuming positive values, the larger
is, the faster the areas accumulate for infinitesimal changes in the input.
In fact, it is a direct proportionality. If is twice as big as
, then the infinitesimal area near
are twice as big as the corresponding infinitesimal areas near
(for the same infinitesimal change
in the input).
Therefore, if , the rate of change of this function at
, namely
, must equal
.
Once again, it takes a long time for this to sink in. It is best thought about in terms of animations.
Revisit the animation of the distance traveled when the speed is farther above.
Since, for instance, and
, infinitesimal areas (distances) near time
are accumulating approximately twice as fast as infinitesimal areas (distances) near time
. We could represent this symbolically as
near
and
near
.
Another way to think of it is this: the graph of the distance traveled function is approximately twice as steep near
as it is near
. In other words, the tangent line has double the slope at
compared to
.
Continuing to think about examples like this will help you to get it. Keep at it!
