The First in a Series of Blog Posts on Baby Rudin

Study Help for Baby Rudin, Part 1.1

Bill Kinney's personal copy of Baby Rudin (Principles of Mathematical Analysis, 3rd edition) — My personal copy of Baby Rudin (Principles of Mathematical Analysis, 3rd edition, by Walter Rudin)

The textbook “Principles of Mathematical Analysis”, by Walter Rudin, is considered a “classic” text on real analysis, the subject that uses rigorous deductive logic to put calculus on a firm foundation.

However, just because it is a “classic”, does not mean it is easy or even helpful for some people. This text, which is called “Baby Rudin” for reasons I will get into shortly, is considered very difficult for beginners. I want to help you learn how to work through it and understand it. In particular, I want to help you learn how to read it, understand its proofs, and successfully complete its exercises.

So, if it’s so difficult, why do mathematics professors use it? The three reasons given below are enough for most mathematicians.

Baby Rudin is very elegant (elegance is considered to be a “cardinal virtue” for mathematical writing),
it has very thought-provoking and challenging exercises (which will help you become a true mathematician when you master them), and
it organizes the key content of the subject in a very logical way (making it an essential reference).

On a more mundane level, some professors use it because their professors used it when they were students.

Blog Posts and Video Lectures on Baby Rudin

This is the first of a series of blog posts that I am writing about this textbook. My purpose is to help you gain insight about the difficult parts of the text. I want to help you through it!

I also plan to eventually do a series of video lectures about the content of Baby Rudin. Look for this content at my YouTube channel, “Bill Kinney Math”. I hope to start this sometime in 2021.

As you might expect, this is a long project that could take me a number of years to complete. But this is what I enjoy doing, and I hope you enjoy it as well.

Who will benefit from this? Certainly it will benefit junior and senior undergraduate mathematics majors, as well as graduate students in mathematics. Ambitious high school students can benefit as well.

However, this content is often also needed for those going to graduate school in other areas. Subjects that come to mind include: physics, engineering, statistics, and economics. In fact, when I took a course in graduate school using this text at the University of Minnesota in the early 1990’s, one of my acquaintances in the class was in graduate school for accounting! I certainly did not expect that accountants would need to know real analysis, but his graduate program required it.

Why is this book called Baby Rudin? As you might guess, it’s because there is a “Papa Rudin” and a “Grandpa Rudin” (or “Big Rudin”). Those books are even more advanced. “Papa Rudin” is about measure theory and Lebesgue integration. And “Grandpa Rudin” is about functional analysis. Both of these subjects were developed in the 20th century, whereas the content of Baby Rudin was mostly developed in the 19th century.

Baby Rudin Pulls a Formula Out of a Hat

One of the most frustrating things about Baby Rudin is that many of the methods and formulas seem to be “pulled out of a hat”. These methods and formulas seem somewhat “magical” and lead you to question yourself: how could I have possibly thought of that?!?

You will encounter such a situation very quickly as you start reading. The first order of business on page 2 is to prove that the square root of 2, written $\sqrt{2}$ , is not rational (it is not an element of the set of rational numbers $\Bbb{Q}$ ). This is done very succinctly with the standard classic and beautiful proof. The details will not be given here.

But next, after letting $A=\left\{p\in \Bbb{Q}: p>0\mbox{ and } p^{2}<2\right\}$ and $B=\left\{p\in \Bbb{Q}: p>0\mbox{ and }p^{2}>2\right\}$ , Rudin then creates a function of $p$ which helps him show that $A$ has no largest element and $B$ has no smallest element. It is the form of this function of $p$ which is mysterious. How did Rudin (or anyone else) know it would work?

The function in question is $q=f(p)=p-\frac{p^{2}-2}{p+2}$ . Using this function, Rudin proves the following statements.

If $p\in A$ , then $q=f(p)>p$ and $q\in A$ . This proves that $A$ has no largest element (because $p$ is an arbitrary element of $A$ ).
If $p\in B$ , then $q=f(p)<p$ and $q\in B$ . This proves that $B$ has no smallest element (because $p$ is an arbitrary element of $B$ ).

Rudin’s purpose in doing this is to illustrate one way that the rational number system $\Bbb{Q}$ is “deficient” or “incomplete”.

Verifying That This Function Works

Before we try to understand where the function $f$ came from (which is the mystery), let’s verify the previous two statements with more detail than Rudin provides.

Proof of Statement 1

Start with statement 1. Assume $p\in A$ . Then, by definition, $p^{2}<2$ . But this means $p^{2}-2<0$ . Furthermore, $p>0$ , so that $p+2>0$ . These two facts then combine to imply that $\frac{p^{2}-2}{p+2}<0$ . And this leads to our first key conclusion that $q=f(p)=p-\frac{p^{2}-2}{p+2}>p$ (subtracting a negative number gives a new quantity that is greater than the old quantity).

Also note that $q=f(p)=\frac{p^{2}+2p-p^{2}+2}{p+2}=\frac{2p+2}{p+2}>0$ .

In addition, $f$ is a rational function with integer coefficients, which implies that if $p\in \Bbb{Q}$ , then $q\in \Bbb{Q}$ . Therefore, the only thing we have left to prove is that $q^{2}<2$ .

Fortunately, this is “set up” (this is the “magic”) so that a direct calculation confirms this fact. Since $f(p)=\frac{2p+2}{p+2}$ , we can confirm that $q^{2}-2<0$ as follows.

$q^{2}-2=(f(p))^{2}-2=\frac{4p^{2}+8p+4-2(p+2)^{2}}{(p+2)^{2}}=\frac{4p^{2}+8p+4-2p^{2}-8p-8}{(p+2)^{2}}=\frac{2(p^{2}-2)}{(p+2)^{2}}<0$

The last inequality holds because $p^{2}-2<0$ and $(p+2)^{2}>0$ .

Proof of Statement 2

Now we prove statement 2. The argument is somewhat of a “mirror image” of the proof of statement 1. Assume $p\in B$ . Then, by definition, $p^{2}>2$ . But this means $p^{2}-2>0$ . Furthermore, $p>0$ , so that $p+2>0$ . These two facts then combine to imply that $\frac{p^{2}-2}{p+2}>0$ . This leads to our first key conclusion that $q=f(p)=p-\frac{p^{2}-2}{p+2}<p$ .

Also note that we can still say that $q=f(p)=\frac{p^{2}+2p-p^{2}+2}{p+2}=\frac{2p+2}{p+2}>0$ .

In addition, as stated before, $f$ is a rational function with integer coefficients, which implies that if $p\in \Bbb{Q}$ , then $q\in \Bbb{Q}$ . Therefore, the only thing we have left to prove is that $q^{2}>2$ .

Once again, a direct calculation will confirm this fact. Since $f(p)=\frac{p^{2}+2p-p^{2}+2}{p+2}=\frac{2p+2}{p+2}$ , we can confirm that $q^{2}-2>0$ as follows.

$q^{2}-2=(f(p))^{2}-2=\frac{4p^{2}+8p+4-2(p+2)^{2}}{(p+2)^{2}}=\frac{4p^{2}+8p+4-2p^{2}-8p-8}{(p+2)^{2}}=\frac{2(p^{2}-2)}{(p+2)^{2}}>0$

The last inequality holds because $p^{2}-2>0$ and $(p+2)^{2}>0$ .

But Where Does This Function Come From?

To see where the function $q=f(p)=p-\frac{p^{2}-2}{p+2}$ comes from, as well as whether any other function would work, it is helpful to list out its key properties used in the arguments above.

If $p\in \Bbb{Q}$ , then $q=f(p)\in \Bbb{Q}$ and if $p>0$ , then $q=f(p)>0$ .
The number $\sqrt{2}$ is a fixed point of $f$ . This means that $f(\sqrt{2})=\sqrt{2}$ .
If $0<p<\sqrt{2}$ , then $0<q<\sqrt{2}$ as well, but $q$ is closer to $\sqrt{2}$ than $p$ is, making $p<q$ . This follows from an argument above, but it also is helpful to try a specific example. Check, for instance, that $f(1.4)\approx 1.41176$ .
If $p>\sqrt{2}$ , then $q>\sqrt{2}$ as well, but $q$ is closer to $\sqrt{2}$ than $p$ is, making $q<p$ . This follows from an argument above, but it also is helpful to try a specific example. Check, for instance, that $f(1.5)\approx 1.42857$ .
The function $g$ defined by $g(p)=(f(p))^2-2$ has $p=\sqrt{2}$ as a root. This follows since $\sqrt{2}$ is a fixed point of $f$ : $g(\sqrt{2})=(f(\sqrt{2}))^{2}-2=(\sqrt{2})^{2}-2=2-2=0$ .
Finally, if $0<p<\sqrt{2}$ , then $g(p)<0$ , while if $p>\sqrt{2}$ , then $g(p)>0$ .

We can illustrate these facts by making graphs of $f$ and $g$ .

The Graph of $q=f(p)$

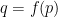
The graph of $q=f(p)=p-\frac{p^{2}-2}{p+2}=\frac{2p+2}{p+2}$ is shown below colored red. It crosses the line $q=p$ at $p=\sqrt{2}$ . This means that $f(\sqrt{2})=\sqrt{2}$ so that $\sqrt{2}$ is a fixed point of $f$ . Also note that, since the slope of $f$ is between 0 and 1, plugging a number $p>0$ into $f$ will result in an output $q$ that is closer to $\sqrt{2}$ than $p$ is. This graphically demonstrates properties 2-4 listed above.

Making an appropriate graph is often a key to help you understand an argument in Baby Rudin. — This graph of $q=f(p)=p-\frac{p^{2}-2}{p+2}=\frac{2p+2}{p+2}$ illustrates properties 2-4 listed above.

The graph of 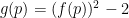$g(p)=(f(p))^{2}-2$

The plot of $g(p)=(f(p))^{2}-2=\frac{2(p^{2}-2)}{(p+2)^{2}}$ is the red graph below. It crosses the horizontal $p$ -axis at $p=\sqrt{2}$ . This means that $\sqrt{2}$ is a root of $g$ . Also note that, since the slope of $g$ is positive, plugging a number $0<p<\sqrt{2}$ into $g$ will result in a negative output, while plugging a number $p>\sqrt{2}$ into $g$ will result in a positive output. This graphically demonstrates properties 5-6 listed above.

*This graph of $g(p)=(f(p))^{2}-2=\frac{2(p^{2}-2)}{(p+2)^{2}}$ illustrates properties 5-6 listed above.*

Is there a Simpler Choice for the Function f?

This leads us to wonder: is there a simpler choice for the function $f$ above? Evidently, we would still want to choose $f$ so that properties 1-6 are still true (where the function $g$ is defined in the same way based on $f$ ).

Property 1 immediately rules out a linear function such as $q=f(p)=\frac{p-\sqrt{2}}{2}=\frac{1}{2}p-\frac{\sqrt{2}}{2}$ . Why? Since $\sqrt{2}\not\in\Bbb{Q}$ , then $p\in \Bbb{Q}$ would imply that, unfortunately, $q=f(p)\not\in \Bbb{Q}$ .

What happens if we try letting $q=f(p)=p-(p^{2}-2)=-p^{2}+p+2$ ? Certainly, $\sqrt{2}$ is a fixed point here. But $f'(p)=-2p+1$ , so that $f'(\sqrt{2})=1-2\sqrt{2}<0$ . This would cause properties 3 and 4 to fail. You can think about this graphically, but also just note that, for example, $f(1.4)=-1.4^{2}+1.4+2=3.4-1.96=1.44>\sqrt{2}$ , whereas $1.4<\sqrt{2}$ .

Next, a bit of experimentation reveals that $q=f(p)=p-\frac{p^{2}-2}{3}=-\frac{1}{3}p^{2}+p+\frac{2}{3}$ might work. After all, $f'(p)=-\frac{2}{3}p+1$ so that $f'(\sqrt{2})=\frac{3-2\sqrt{2}}{3}\approx 0.057$ , implying that $0<f'(\sqrt{2})<1$ . However, we still have a problem in that $f'(p)<0$ if $p>\frac{3}{2}=1.5$ . Technically this means property 4 could fail for $p>\frac{3}{2}$ . Maybe this is not a big deal (maybe we only need property 4 to hold true in this case for $\sqrt{2}<p<\frac{3}{2}$ ), but the argument could become more convoluted because of it.

Modified Choices of f

It is becoming clear that maybe $f$ cannot be chosen to be much simpler. We do not want our argument to become too convoluted. However, we might wonder whether any function of the form $q=f(p)=p-\frac{p^{2}-2}{p+k}$ will work when, presumably, $k>0$ and $k\in \Bbb{Q}$ . In particular, is it truly necessary to choose $k=2$ ?

Let us do calculations to help us see whether this is true or not. First note that such a function $f$ maps rationals to rationals (if $p\in \Bbb{Q}$ , then $q=f(p)\in \Bbb{Q}$ ). Also note that $f(\sqrt{2})=\sqrt{2}$ , irrespective of the value of $k$ .

Furthermore, $f(p)=\frac{p^{2}+kp-p^{2}+2}{p+k}=\frac{kp+2}{p+k}$ . Using the Quotient Rule, we can then compute $f'(p)=\frac{(p+k)k-(kp+2)}{(p+k)^{2}}=\frac{k^{2}-2}{(p+k)^{2}}$ . From this, we see that $f'(p)>0$ for all $p>0$ if and only if $k^{2}-2>0$ . Since $k>0$ , this is equivalent to $k>\sqrt{2}$ .

Hey! The number 2 is the least positive integer greater than $\sqrt{2}$ ! That’s probably why Rudin chose $k=2$ !!! Insight! Yay!!

On the other hand, we might wonder if the slope of the graph of $f$ gets too big when $k$ gets larger and larger (which could cause properties 3 and 4 to fail because $q$ would be further away from $\sqrt{2}$ than $p$ is).

No matter what $k>\sqrt{2}$ is, the slope of the graph of $f$ is maximized at $p=0$ and equals $f'(0)=\frac{k^{2}-2}{k^{2}}=1-\frac{2}{k^{2}}.$ But this is a quantity that is clearly less than 1 for all $k>\sqrt{2}$ .

But What About the Function g?

What happens with the function $g(p)=(f(p))^{2}-2$ for various values of $k$ ? Clearly, $p=\sqrt{2}$ is still a root of $g$ , making property 5 satisfied. And, for a general value of $k$ , we get $g(p)=\frac{k^{2}p^{2}+4kp+4-2(p^{2}+2kp+k^{2})}{(p+k)^{2}}.$ But this implies that $g(p)=\frac{(k^{2}-2)p^{2}+4-2k^{2}}{(p+k)^{2}}=\frac{(k^{2}-2)(p^{2}-2)}{(p+k)^{2}}$ .

I’ll leave it as an exercise for you to do with the Quotient Rule to confirm that $g'(p)=\frac{(k^{2}-2)(2kp+4)}{(p+k)^{3}}$ . Then, because of this, if $k>\sqrt{2}$ so that $k^{2}-2>0$ , it follows that $g'(p)>0$ for all $p>0$ . This will imply that property 6 is satisfied.

Here is an animation of the graphs of both $f(p)$ and $g(p)$ as $k$ increases from 1.5 to 5. Properties 1-6 are all satisfied!

Graphing families of functions can show you that many choices of parameters are possible. The choice made in Baby Rudin can be considered to be the simplest. — The graphs of both $f(p)$ and $g(p)$ as $k$ increases from 1.5 to 5. Properties 1-6 are all satisfied!

The graphs of both $f(p)$ and $g(p)$ as $k$ increases from 1.5 to 5. Properties 1-6 are all satisfied!

We conclude by remarking that $q= f(p)=\frac{kp+2}{p+k}$ gets closer to $\sqrt{2}$ than $p>0$ is when $k>\sqrt{2}$ because $\sqrt{2}$ is a so-called attracting fixed point of the function (“mapping”) $f$ . An appropriate cobweb plot will help you see this. It’s very much related to the fact that $0<f'(p)<1$ for all $p>0$ when $k>\sqrt{2}$ .

2 Replies to “Baby Rudin: Let Me Help You Understand It!”

Diego says:

January 10, 2021 at 5:38 am

Dear Prof. Kinney,

An excellent idea to endevour in this project.

I wish you most of success and I will be following closely the Blog posts. I have tried many times to got my self through the book. Then comes the point where I get discouraged because I don’t know if I understand the idea correctly and therefore can’t objectively evaluate my solutions to the problems.

The topics covered in the book are indeed fundamental if one wants to understand more advanced and modern topics in Mathematics, for example partial differential equations or non linear differential equations. Fundamental topics for engineering too!

Best of success and thank you very much.
Best regards,
Diego.
Pingback: Definitions of Ordered Set and Ordered Field - Infinity is Really Big

Comments are closed.