And an Ordered Field That Can Be Ordered in More Than One Way

Study Help for Baby Rudin, Part 1.2

A visual for a totally ordered set with three elements. — A graphic representation of the totally ordered set of three points $\left\{a,b,c\right\}$ with $a<b<c$ . The directed line segments are not part of the set. They only indicate the order.

A graphic representation of the totally ordered set of three points $\left\{a,b,c\right\}$ with $a<b<c$ . The directed line segments are not part of the set. They only indicate the order.

The set of real numbers 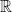$\Bbb{R}$ is more than just a set. As we learn at a young age, we can visualize the real numbers using the real number line, implicitly implying that they are “ordered”. The real numbers also have the algebraic structure of a mathematical field, in which we can add and multiply according to the usual rules. In fact, the real numbers form an ordered field.

The set of real numbers has a field structure, under the operations of ordinary addition and ordinary multiplication. The set of real numbers is also a totally ordered set. Taken together, these facts are almost enough to mean the real numbers form an ordered field.

However, we cannot impose a (total) order on the real number field in any way we want. In order to be an ordered field, the algebraic field properties and the order must be “compatible” in certain special ways.

What are these ways?

If the same number is added to both sides of an inequality, then the inequality symbol, either $<$ or $>$ , should stay in the same direction. That is, if $y<z$ , then $x+y<x+z$ .
The product of two positive numbers should be positive. That is, if $x>0$ and $y>0$ , then $xy>0$ .

The number zero plays a special role in defining which numbers are positive and which numbers are negative to begin with. Many textbooks in Real Analysis approach this topic axiomatically. They assume that the set of positive real numbers $P$ are, in part, characterized by the property that $x,y\in P\Rightarrow x+y\in P\mbox{ and } xy\in P$ .

Where Are These Topics Found in Baby Rudin?

In “Principles of Mathematical Analysis”, Third Edition, by Walter Rudin (a.k.a., Baby Rudin), these topics are addressed on pages 3-8. Also found on these pages is the crucial concept that the ordered field of real numbers $\Bbb{R}$ is complete. I will discuss this topic in-depth in later posts. It is the key feature that distinguishes the real numbers from, for example, the rational numbers.

While Baby Rudin takes a very precise approach to many of the topics in Real Analysis, for the concept of an ordered set, it is less precise than many other texts. In order to open your mind to other possibilities and help you realize when definitions are not as precise as they could be, it will be useful for us to consider the precise definition of an ordered set in this article.

Definition of an Order on a Set and an Ordered Set

Suppose $S$ represents a nonempty set. In Baby Rudin, an order on $S$ is defined to be a (binary) relation, denoted by $<$ , with two properties:

If $x\in S$ and $y\in S$ , then one and only one of the statements $x<y, x=y, \mbox{ or } y<x$ is true (“trichotomy”). This also means that any two distinct elements are “comparable” (contrast this with the concept of a partially ordered set, or “poset”).
If $x,y,z\in S$ , and if $x<y$ and $y<z$ , then $x<z$ (“transitivity”).

In addition, Baby Rudin defines $x\leq y$ to mean either $x<y$ or $x=y$ . Furthermore, $y>x$ is another way to write $x<y$ and $y\geq x$ is another way to write $x\leq y$ .

A set $S$ is called an ordered set if an order is defined on it.

So What is Wrong With This Definition of an Order on a Set?

You might wonder: what is wrong with this definition? Why is it not precise?

The main reason it is not precise is that the notion of a (binary) relation on a set has not been defined. In addition, we are understanding the word “set” from the perspective of “naive set theory”. Naive set theory has its own problems, which we will not get into (it leads to paradoxes).

Most textbooks in Real Analysis wisely avoid trying to “fix” naive set theory. That is, they avoid approaching it from an axiomatic point of view. However, it is probably worthwhile to at least define the concept of a relation here. This is based on the naive view of a set as a collection of “objects” (whatever those objects might be).

Cartesian Products, Relations, and Orders

We need a preliminary concept. Given any two sets $A$ and $B$ , we define the Cartesian product $A\times B$ of $A$ and $B$ to be the set of all ordered pairs $A\times B=\left\{(a,b)\ |\ a\in A\mbox{ and }b\in B\right\}$ . Note that the first “coordinate” of $(a,b)$ must be from the set $A$ and the second “coordinate” of $(a,b)$ must be from the set $B$ . Also note that, if $A\not=B$ , then $A\times B\not=B\times A$ (they are different sets).

Definition: A (binary) relation $R$ on a set $S$ is a subset of the Cartesian product $S\times S$ . When $(x,y)\in R$ , it is common to also write $xRy$ (i.e., “ $x$ is related to $y$ “).

That’s it! A relation on a set is just a subset of the Cartesian product of the set with itself. (I will avoid including the word “binary” from now on; evidently, there are other kinds of relations that can be defined on a set as well.)

So what, then, is an order $<$ on a set $S$ ? It’s a special kind of relation on $S$ .

Definition: An order on a set $S$ is a relation $R$ on $S$ that also satisfies the following properties: 1) If $x,y\in S$ , then one and only one of the statements $xRy,$ $x=y,$ or $yRx$ is true (“trichotomy”). And 2) If $x,y,z\in S$ and if $xRy$ and $yRz$ , then $xRz$ (“transitivity”).

From now on, we write $x<y$ in place of $xRy$ for an order on $S$ . In other words, technically-speaking, the symbol $<$ represents a special kind of subset of $S\times S$ . Also note how this definition jibes with the definition in Baby Rudin written further above.

Example 1: An Order on a Finite Set

It is probably best at this point to give a simple example. Let $S=\left\{a,b,c\right\}$ . Define an order $<$ on $S$ to be the set:

$<=\left\{(a,b),(b,c),(a,c)\right\}$ (i.e, $<$ equals this 3 element set)

Note that $<$ is certainly a subset of $S\times S=\left\{(a,a),(a,b),(a,c),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c)\right\}$ . You should check that the definition of an order is satisfied by the set $<$ here.

As sets, $<$ and $S\times S$ can be visualized as points in a “plane”, where the elements of $S$ are on the “axes”.

Do not take this too literally because $a$ , $b$ , and $c$ might not be numbers. However, it can still be a helpful tool for our imaginations.

This is one way to visualize an order as a special relation which is a subset of a Cartesian product S x S. The set S is not an ordered field, however. — The Cartesian product $S\times S$ can be imagined as the collection of all 9 points. The order $<$ is the subset of the 3 points that are drawn bigger than the others.

The Cartesian product $S\times S$ can be imagined as the collection of all 9 points. The order $<$ is the subset of the 3 points that are drawn bigger than the others.

We can also visualize this ordered set as three points on a “line” (i.e., vertices on a linear “directed graph”), as shown in the picture at the very top of this post. The directed line segments themselves are not part of the set — they only indicate the direction of the ordering ( $a$ is less than $b$ is less than $c$ ).

Based on this order on $S$ , it would also make sense to write

$\leq =\left\{(a,a),(b,b),(c,c),(a,b),(b,c),(a,c)\right\}$ (i.e, $\leq$ equals this 6 element set)

Don’t let it bother you that the letters in this set are just pure symbols. We don’t have to think of about orders in terms of relations between numbers. For example, the letters could represent foods that you want to eat at a meal, while the order could represent the order you want to eat them in.

We can also define other orders on $S$ . Another example is $<=\left\{(b,a),(a,c),(b,c)\right\}$ . In fact, there are $3!=3\cdot 2\cdot 1=6$ distinct (total) orders that can be defined on any set with 3 elements.

Ordered Fields

In a nutshell, a nonempty set $F$ is called a field if there are two binary operations defined of $F$ , typically called addition $+$ and multiplication $\times$ (or $\cdot$ ), such that all the “standard” properties you learn in school hold true for these operations (closure, associativity, commutativity, etc…). The most common fields encountered by students in school are the rational numbers $\Bbb{Q}$ , the real numbers $\Bbb{R}$ , and the complex numbers $\Bbb{C}$ (under the “standard” definitions of addition and multiplication). We could give a full list of all the field properties here, but we will save that for another post.

Are there any finite fields? There most certainly are.

Example 2: a Field with Two Elements

The simplest finite field is the two-element set $\Bbb{Z}_{2}=\left\{0,1\right\}$ . In this field, we define addition by the equations $0+0=0, 0+1=1+0=1,$ and $1+1=0$ . We define multiplication by the equations $0\cdot 0=0, 0\cdot 1=1\cdot 0=0,$ and $1\cdot 1=1$ . These operations are called “mod 2 arithmetic”.

There are two possible orders on $\Bbb{Z}_{2}$ . The most “natural” one is $<=\left\{(0,1)\right\}$ (That’s it! This is a one-element subset of the Cartesian product $\Bbb{Z}_{2}\times \Bbb{Z}_{2}=\{(0,0),(1,0),(0,1),(1,1)$ ). This means that $0<1$ .

However, now we ask whether this order is “compatible” with the field properties as discussed at the beginning of this article. That is, if the same element is added to both sides of a valid inequality, does the inequality stay the same “direction”?

The answer is no. Note that $0<1$ , but $0+1\not< 1+1$ because $1\not< 0$ (i.e., $1>0$ ).

This is a partial argument for why $\Bbb{Z}_{2}$ cannot be defined to be an ordered field (though it certainly can be defined to be an ordered set). In fact, no finite field can be an ordered field.

Example 3: the Rational Numbers Form an Ordered Field

Since each rational number is a real number, each rational number corresponds to a unique point on a real number line. It therefore seems natural to hope that the “standard” order on $\Bbb{R}$ , “imposed” on $\Bbb{Q}$ , will make $\Bbb{Q}$ into an ordered field. Since we need to have some starting point, we will assume that we know what it means for an arbitrary integer (element of the “ring” $\Bbb{Z}$ ) to be positive or negative or zero.

Given two distinct rational numbers $\frac{m}{n},\frac{p}{q}\in \Bbb{Q}$ , say in lowest terms with $n$ and $q$ taken to be positive integers, how should we determine the truth value (true or false) of the statement $\frac{m}{n}<\frac{p}{q}$ ?

It seems reasonable to define that if $m\leq 0$ and $p>0$ , or if $m<0$ and $p\geq 0$ , then $\frac{m}{n}<\frac{p}{q}$ , so we do so. Note that this also means that $0=\frac{0}{1}<\frac{m}{n}$ if and only if $m>0$ , and that $\frac{m}{n}<0=\frac{0}{1}$ if and only if $m<0$ .

But what if $m$ and $p$ are either both positive or both negative? Think about it in terms of “cross-multiplication”. We should define $\frac{m}{n}<\frac{p}{q}$ if and only if $mq<np$ (the inequality should not change direction after multiplying since each integer is positive). But this is true if and only if $np-mq>0$ . This last inequality on the integers will be how we define $\frac{m}{n}<\frac{p}{q}$ to be true when $m$ and $p$ are both positive. In other words, in this case, we say that $\frac{m}{n}<\frac{p}{q}$ if and only if $np-mq>0$ .

The case where $m$ and $p$ are both negative is handled with the same inequality, namely $np-mq>0$ . The reason is that after “cross-multiplying” by two negative integers, the inequality should still end up in the same direction.

Is This Order Compatible with the Field Properties?

Now we ask: is this ordering compatible with the field properties? Once again, we assume we know all about how arithmetic and inequalities work in the ring $\Bbb{Z}$ . We also assume we know how to add and multiply rational numbers.

Certainly the product of two positive rational numbers is positive. If $m>0$ and $p>0$ , then $\frac{m}{n}\cdot \frac{p}{q}=\frac{mp}{nq}>0$ . This is because the product of two positive integers is known to be positive.

For the other condition, let’s just consider the case where all the rational numbers (and all the integers) involved are positive. You can consider the other cases on your own.

Assume that $\frac{m}{n}<\frac{p}{q}$ and that $\frac{r}{s}\in \Bbb{Q}$ with $r,s>0$ (also, $m,n,p,q>0$ ). We want to prove that $\frac{m}{n}+\frac{r}{s}<\frac{p}{q}+\frac{r}{s}$ .

Our assumption implies that $np-mq>0$ . By the definition of addition in $\Bbb{Q}$ , we can write $\frac{m}{n}+\frac{r}{s}=\frac{ms+nr}{ns}$ and $\frac{p}{q}+\frac{r}{s}=\frac{ps+qr}{qs}$ . This means we want to prove that $ns(ps+qr)-qs(ms+nr)>0$ .

But this is easy. We can compute $ns(ps+qr)-qs(ms+nr)=nps^{2}+nqrs-mqs^{2}-nqrs=(np-mq)s^{2}$ . But $np-mq>0$ and $s^2>0$ . Therefore, $ns(ps+qr)-qs(ms+nr)>0$ so that $\frac{m}{n}+\frac{r}{s}<\frac{p}{q}+\frac{r}{s}$ .

Actually, this argument works with no restrictions on $r$ and $s$ as long as we don’t divide by zero to form the fraction $\frac{r}{s}$ .

the real numbers form an Ordered field

For the moment, we will not define the “standard” order on the field of real numbers $\Bbb{R}$ that makes it an ordered field. In fact, we are also not defining how to add and multiply real numbers at the moment either.

But here’s a question. Is there only one order we can define on $\Bbb{R}$ to make it an ordered field? The answer is “yes”, with a mild caveat. It is true “up to (order-preserving) isomorphism”. See https://math.ucr.edu/~res/math205A/uniqreals.pdf for more detail. Suffice it to say that we will take the answer to be “yes”.

Definition of an Ordered Field

Here is a formal definition of an ordered field which is equivalent to the definition given on page 7 of Baby Rudin. For this article, we are still not fully defining what a field is.

Definition: Let $F$ be a field. We say that $F$ is an ordered field if it is an ordered set (with order $<$ ) and the following conditions are true. (i) If $x,y,z\in F$ and $y<z$ , then $x+y<x+z$ . (ii) If $x,y\in F$ with $x>0$ and $y>0$ , then $xy>0$ .

As stated above, the ordering on the real number field $\Bbb{R}$ is essentially unique. But we might wonder. Do there exist other ordered fields which have two distinct (non-isomorphic) compatible orders?

An Ordered Field with Two Distinct Compatible Orders

You should always strive to be familiar with many “counterexamples” in a subject like Real Analysis. A counterexample is an example that disproves a mathematical statement. In other words, a counterexample is an example that shows that a given (necessarily false) statement is indeed false. Oftentimes the false statement might, at first glance, “seem” to be true. That’s what makes counterexamples a truly necessary part of your education in mathematics. They can correct faulty intuition and show you where you need to be more careful.

Here’s a simple example of a false statement that might seem to be true at first glance: if $x^{2}=25$ , then $x=5$ . This is indeed a false statement: the number $x=-5$ is a counterexample.

If you really want to understand Real Analysis deeply, I highly recommend getting the book “Counterexamples in Analysis”, by Bernard Gelbaum and John Olmsted. On page 14 of that book you will find an example of a field that is an ordered field in two distinct ways. Let’s explore this example now.

Example 4: The Rationals with the square root of 2 adjoined

Let $S=\Bbb{Q}(\sqrt{2})=\left\{a+b\sqrt{2}\ |\ a,b\in \Bbb{Q}\right\}$ (note that I’m not bothering to write $a$ and $b$ as fractions). This set is indeed a field under ordinary addition and multiplication. It is often informally described as “the rationals adjoined with the square root of 2”. It is the “smallest” field extension of $\Bbb{Q}$ containing the number $\sqrt{2}$ .

In $\Bbb{Q}(\sqrt{2})$ , we add and multiply numbers as you would expect: $(a+b\sqrt{2})+(c+d\sqrt{2})=(a+c)+(b+d)\sqrt{2}$ and $(a+b\sqrt{2})(c+d\sqrt{2})=(ac+2bd)+(ad+bc)\sqrt{2}$ . It is important to also note that every nonzero element in $\Bbb{Q}(\sqrt{2})$ has a multiplicative inverse that is also in $\Bbb{Q}(\sqrt{2})$ . To see this, note that $\frac{1}{a+b\sqrt{2}}=\frac{a-b\sqrt{2}}{a^{2}-2b^{2}}=\frac{a}{a^{2}-2b^{2}}+\frac{-b}{a^{2}-2b^{2}}\sqrt{2}$ , where $a^{2}-2b^{2}\not=0$ since $a,b\in \Bbb{Q}$ with either $a\not=0$ or $b\not=0$ , and since $\sqrt{2}\not\in\Bbb{Q}$ .

The standard way to define an order $\Bbb{Q}(\sqrt{2})$ is to use the order it inherits as a subfield of the real numbers $\Bbb{R}$ . This amounts to defining $a+b\sqrt{2}<c+d\sqrt{2}$ if and only if $(c-a)+(d-b)\sqrt{2}>0$ .

However, there is another (non-isomorphic) order, call it $<^{*}$ , that can be defined on $\Bbb{Q}(\sqrt{2})$ . We define $a+b\sqrt{2}<^{*}c+d\sqrt{2}$ if and only if $(c-a)-(d-b)\sqrt{2}=(c-a)+(b-d)\sqrt{2}>0$ , where $>$ represents the standard order (written in the opposite direction) on $\Bbb{Q}(\sqrt{2})$ (and on $\Bbb{R}$ ). Note the subtle difference between the definitions of $<$ and $<^{*}$ .

We should check that $\Bbb{Q}(\sqrt{2})$ is still an ordered field with respect to $<^{*}$ .

Check Condition (i)

Let $a+b\sqrt{2}, c+d\sqrt{2}, e+f\sqrt{2}\in \Bbb{Q}(\sqrt{2})$ and assume that $c+d\sqrt{2}<^{*}e+f\sqrt{2}$ . We want to show that $(a+b\sqrt{2})+(c+d\sqrt{2})<^{*}(a+b\sqrt{2})+(e+f\sqrt{2})$ .

The fact that $c+d\sqrt{2}<^{*}e+f\sqrt{2}$ implies that $(e-c)+(d-f)\sqrt{2}>0$ . Since $(a+b\sqrt{2})+(c+d\sqrt{2})=(a+c)+(b+d)\sqrt{2}$ and $(a+b\sqrt{2})+(e+f\sqrt{2})=(a+e)+(b+f)\sqrt{2}$ , we must show that $((a+e)-(a+c))+((b+d)-(b+f))\sqrt{2}>0$ .

But this is easy: $((a+e)-(a+c))+((b+d)-(b+f))\sqrt{2}=(e-c)+(d-f)\sqrt{2}>0$ . Therefore, condition (i) is satisfied.

Check Condition (ii)

Now assume $a+b\sqrt{2}, c+d\sqrt{2} \in \Bbb{Q}(\sqrt{2})$ and that $0<^{*}a+b\sqrt{2}$ and $0<^{*}c+d\sqrt{2}$ . We want to prove that $0<^{*}(a+b\sqrt{2})(c+d\sqrt{2})$ .

The facts that $0=0+0\sqrt{2}<^{*}a+b\sqrt{2}$ and $0=0+0\sqrt{2}<^{*}c+d\sqrt{2}$ imply that $a-b\sqrt{2}>0$ and $c-d\sqrt{2}>0$ . Since $(a+b\sqrt{2})(c+d\sqrt{2})=(ac+2bd)+(ad+bc)\sqrt{2}$ , we must show that $(ac+2bd)-(ad+bc)\sqrt{2}>0$ .

But this is easy as well: it follows because $(a-b\sqrt{2})(c-d\sqrt{2})=(ac+2bd)+(-ad-bc)\sqrt{2}=(ac+2bd)-(ad+bc)\sqrt{2}$ and because $(a-b\sqrt{2})(c-d\sqrt{2})>0$ . Therefore, condition (ii) is satisfied.

Can This Order Be Visualized?

You might wonder: can this order $<^{*}$ on $\Bbb{Q}(\sqrt{2})=\left\{a+b\sqrt{2}\ |\ a,b\in \Bbb{Q}\right\}$ be visualized?

First of all, we should realize that, even though $\Bbb{Q}(\sqrt{2})\subseteq \Bbb{R}$ is a subset of the real number line, if we want, we can visualize $\Bbb{Q}(\sqrt{2})$ as being a subset of the “rational coordinate plane” $\Bbb{Q}^{2}=\Bbb{Q}\times \Bbb{Q}\subseteq \Bbb{R}\times \Bbb{R}=\Bbb{R}^{2}$ (the $\times$ symbols represent Cartesian products, as defined further above).

How? It’s analogous to how complex numbers can be visualized in the complex plane. Associate each number $a+b\sqrt{2}\in \Bbb{Q}(\sqrt{2})$ with the point $(a,b)\in \Bbb{Q}^{2}$ (with rational coordinates). In other words, we could think of the horizontal axis as the “rational axis” (as a subset of the real $x$ -axis) and the vertical axis as the “irrational axis” (as a subset of the real $y$ -axis). The “rational part” of $a+b\sqrt{2}$ would then be $a\in \Bbb{Q}$ , while the “irrational part” of $a+b\sqrt{2}$ would then be $b\in \Bbb{Q}$ (just as the imaginary part of a complex number is a real number).

Though this might seem strange, it is actually a very natural thing to do. If you’re interested, it also turns out that this association is “structure-preserving” in that it defines an isomorphism of vector spaces over the field $\Bbb{Q}$ .

Visualizing the Standard Order

Since the condition $x+y\sqrt{2}>0$ is equivalent to $y>-\frac{x}{\sqrt{2}}$ , the (linear) transformation $L_{<}:\Bbb{Q}^{2}\longrightarrow \Bbb{R}^{2}$ defined by $L_{<}(x,y)=(x+y\sqrt{2},0)$ maps all the points in $\Bbb{Q}^{2}$ above the line $y=-\frac{x}{\sqrt{2}}$ to the positive horizontal axis and all the points in $\Bbb{Q}^{2}$ below the line $y=-\frac{x}{\sqrt{2}}$ to the negative horizontal axis. In other words, in $\Bbb{Q}^{2}$ , the “positives” with respect to $<$ are above that line and the “negatives” with respect to $<$ are below that line. The only point of $\Bbb{Q}^{2}$ that is actually on the line $y=-\frac{x}{\sqrt{2}}$ is the origin $(0,0)$ , which gets mapped to itself.

As a mapping from $\Bbb{Q}^{2}$ to the $\Bbb{Q}(\sqrt{2})\times \left\{0\right\}$ (part of the horizontal axis), the function $L_{<}$ is not only onto, but is also one-to-one. It is also clear that $L_{<}^{-1}(x+y\sqrt{2},0)=(x,y)$ .

We can picture this as shown below. Note that the transformation maps points to the horizontal axis parallel to the line $y=-\frac{x}{2}$ . This means that the points end up the same (signed) horizontal distance from the line $y=-\frac{x}{2}$ that they started with. This horizontal signed distance, even at the start, is the true “numerical value” of $a+b\sqrt{2}$ (as a rational number when $b=0$ and an irrational number when $b\not=0$ ).

Here is a way to visualize the rationals adjoined with the square root of two as an ordered field in the standard order it inherits from the field of real numbers. — The field $\Bbb{Q}(\sqrt{2})$ can be visualized as an ordered field, with respect to the order $<$ it inherits as a subfield of $\Bbb{R}$ , in two ways. First, it can be visualized as a subset of the real line (think of the real line as the “full” horizontal axis in the picture). Second, it can be visualized as a subset of $\Bbb{Q}^{2}=\Bbb{Q}\times \Bbb{Q}$ . The mapping shown relates positives and negatives with respect to this order.

Visualizing the Non-Standard Order

For the non-standard order $<^{*}$ , we can still visualize $\Bbb{Q}(\sqrt{2})$ as a plane in the same way, through the association $(a,b)\leftrightarrow a+b\sqrt{2}$ . However, the locations of the positive and negative points changes (because the positive and negative numbers themselves change) as well as how the points get mapped to on the horizontal axis. This then changes where we imagine the positive and negative numbers of $\Bbb{Q}(\sqrt{2})$ to “live” as a subset of the real line $\Bbb{R}$ .

The condition $0<^{*} x+y\sqrt{2}$ is equivalent to $x-y\sqrt{2}>0$ , which is equivalent to $y<\frac{x}{\sqrt{2}}$ . Therefore, the (linear) transformation $L_{<^{*}}:\Bbb{Q}^{2}\longrightarrow \Bbb{R}^{2}$ defined by $L_{<^{*}}(x,y)=(x-y\sqrt{2},0)$ maps all the points in $\Bbb{Q}^{2}$ below the line $y=\frac{x}{\sqrt{2}}$ to the positive horizontal axis and all the points in $\Bbb{Q}^{2}$ above the line $y=\frac{x}{\sqrt{2}}$ to the negative horizontal axis. In other words, in $\Bbb{Q}^{2}$ , the “positives” with respect to $<^{*}$ are below that line and the “negatives” with respect to $<^{*}$ are above that line. As before, the origin $(0,0)$ is the only point in $\Bbb{Q}^{2}$ on the line itself and it gets mapped to itself.

As before, as a mapping from $\Bbb{Q}^{2}$ to the $\Bbb{Q}(\sqrt{2})\times \left\{0\right\}$ (part of the horizontal axis), the function $L_{<^{*}}$ is not only onto, but is also one-to-one. It is also clear that $L_{<^{*}}^{-1}(x-y\sqrt{2},0)=(x,y)$ .

We can picture this as shown below. Note that the transformation maps points to the horizontal axis parallel to the line $y=\frac{x}{2}$ . This means that the points end up the same (signed) horizontal distance from the line $y=\frac{x}{2}$ that they started with. This horizontal signed distance, even at the start, is the true “numerical value” of $a+b\sqrt{2}$ (as a rational number when $b=0$ and an irrational number when $b\not=0$ ).

The field $\Bbb{Q}(\sqrt{2})$ can be visualized as an ordered field, with respect to the non-standard order $<^{*}$ , in two ways. First, it can be visualized as a subset of the real line (think of the real line as the “full” horizontal axis in the picture). Second, it can be visualized as a subset of $\Bbb{Q}^{2}=\Bbb{Q}\times \Bbb{Q}$ . The mapping shown relates positives and negatives with respect to this order.

Numbers That Are Positive With Respect to Both Orders

There are certainly numbers in $\Bbb{Q}(\sqrt{2})$ that are positive with respect to both orders. Visually, these are the numbers that are in the intersection of the blue regions from both figures above. In other words, these are the numbers corresponding to points $(x,y)\in \Bbb{Q}^{2}$ in the wedge where $x>0$ and $-\frac{x}{\sqrt{2}}<y<\frac{x}{\sqrt{2}}$ . There are also, of course, numbers that will be negative with respect to both orders.

Relating the Visuals

How should we relate these visuals? In other words, if we imagine a point $a+b\sqrt{2}\in \Bbb{Q}(\sqrt{2})$ as being on the real line (i.e., being in the set $\Bbb{Q}(\sqrt{2})\times \left\{0\right\}$ ) with respect to the standard order $<$ , where will it be with respect to the new order $<^{*}$ ?

We can think about this in terms of the transformations $L_{>}$ and $L_{>^{*}}$ . Start with a number $a+b\sqrt{2}\in \Bbb{Q}(\sqrt{2})$ . With respect to the standard order $<$ , we initially visualize this as the point $(a+b\sqrt{2},0)\in \Bbb{Q}(\sqrt{2})\times \left\{0\right\}$ . We then compute $L_{<}^{-1}(a+b\sqrt{2},0)=(a,b)\in \Bbb{Q}^{2}$ (map it away from the horizontal axis and parallel to the line $y=-\frac{x}{2}$ ). From there, we find $L_{<^{*}}(a,b)=(a-b\sqrt{2},0)\in \Bbb{Q}(\sqrt{2})\times \left\{0\right\}$ (map it back to the horizontal axis and parallel to the line $y=\frac{x}{\sqrt{2}}$ .

What is the net effect of this composition? It maps $(a+b\sqrt{2},0)\in \Bbb{Q}(\sqrt{2})\times \left\{0\right\}$ to $(a-b\sqrt{2},0)\in \Bbb{Q}(\sqrt{2})\times \left\{0\right\}$ .

However, the geometric effect of this composition is not very clear, because it depends on the values of both $a$ and $b$ . Two numbers in $\Bbb{Q}(\sqrt{2})$ could be “close together” under $<$ but relatively “far apart” under $<^{*}$ .

For example, $-3+4\sqrt{2}\approx 2.66$ and $2+0.5\sqrt{2}\approx 2.71$ are close together (within about 0.05 units) under $<$ . But $L_{<^{*}}(L_{<}^{-1}(-3+4\sqrt{2},0))=(-3-4\sqrt{2},0)\approx (-8.66,0)$ and $L_{<^{*}}(L_{<}^{-1}(2+0.5\sqrt{2},0))=(2-0.5\sqrt{2},0)\approx (1.29,0)$ are relatively far apart (about 9.95 units) under $<^{*}$ .

This means it is tough to tell where a point will end up under the composition of these transformations just by looking at its initial location on the number line. You really do need to know the values of $a$ and $b$ in the expression $a+b\sqrt{2}$ .

On the other hand, if you increase or decrease the numerical value of $a+b\sqrt{2}$ just by changing either the rational part $a$ alone or the irrational part $b$ alone (don’t change them both at the same time), then it is easier to see what will happen. Increasing $a$ alone will make the number larger with respect to both $<$ and $<^{*}$ . Increasing $b$ alone will make the number larger with respect to $<$ , but smaller with respect to $<^{*}$ .

In the end, the points do indeed get “mixed up” under the composition. It is definitely difficult to fully visualize.

You might ask: what happens to the other real numbers that are not in $\Bbb{Q}(\sqrt{2})$ in this visual? The happy answer is that you don’t need to worry about them. This visual is for $\Bbb{Q}(\sqrt{2})$ alone. You can effectively just pretend the other real numbers don’t exist in the final visualizations described above.

Bonus Material: Relationship to Field Extensions and Galois Theory

If you know about field extensions and Galois theory, you should recognize the mapping $\alpha:\Bbb{Q}(\sqrt{2})\longrightarrow \Bbb{Q}(\sqrt{2})$ defined by $\alpha(a+b\sqrt{2})=a-b\sqrt{2}$ as being a nontrivial element of the Galois group $\mbox{Gal}\left(\Bbb{Q}(\sqrt{2})/\Bbb{Q}\right)$ (of the field extension $\Bbb{Q}(\sqrt{2})$ over $\Bbb{Q}$ ). In fact, it is the only nontrivial element of the Galois group. In other words, $\mbox{Gal}\left(\Bbb{Q}(\sqrt{2})/\Bbb{Q}\right)$ is isomorphic to the additive group $\Bbb{Z}_{2}$ .

But even though $\alpha$ is an isomorphism of $\Bbb{Q}(\sqrt{2})$ to itself (also called an automorphism of $\Bbb{Q}(\sqrt{2})$ ), what we have just seen above is that $\alpha$ does not preserve the order structure of $\Bbb{Q}(\sqrt{2})$ as an ordered field. It is not an “ordered field isomorphism”.

For example, $1.9+2.08\sqrt{2}\approx 4.84156>4.82843\approx 2+2\sqrt{2}$ , but $\alpha(1.9+2.08\sqrt{2})=1.9-2.08\sqrt{2}\approx -1.04156<-0.828427\approx 2-2\sqrt{2}=\alpha(2+2\sqrt{2}).$

The relation $<^{*}$ can also be defined in terms of $\alpha$ . In fact, we can say that $0<^{*} a+b\sqrt{2}$ if and only if $0<\alpha(a+b\sqrt{2})=a-b\sqrt{2}$ .

Evidently, something similar will happen for any field extension of $\Bbb{Q}$ of the form $\Bbb{Q}(\sqrt{n})$ , where $n$ is a positive integer which is not a perfect square.

5 Replies to “Definitions of Ordered Set and Ordered Field”

Diego says:

January 22, 2021 at 1:27 pm

Thank you for the nice Post Prof. Kinney. Great to read the second post!

I have some questions.

1. L<* is not isomorphic to L< right? Eventhough L<* by itself is an isomorphism from Q2 to R2 .?

2. \alpha does not preserve the order structure of \Bbb{Q}(\sqrt{2}) as an ordered field, with it's original order meaning that for x<y the following is flase: \alpha(x) , but in theory one can define it’s own order relation in such a case one could make \alpha ordered w.r.t. the order i.e. L*<?

Many thanks. Best regards,
Diego.
1. Bill says:
  
  January 22, 2021 at 3:09 pm
  
  The L<* and L< are just mappings. They can be thought of as isomorphisms of Q x Q and Q(sqrt(2)) as vector spaces over Q. I'm not quite sure what you are asking on #2. I need to rewrite the blog post at the end to make it more clear, but a + b*sqrt(2) *> 0 if and only if alpha(a + b*sqrt(2)) = a – b*sqrt(2) > 0.
Diego says:

January 22, 2021 at 4:10 pm

Something happened with the post, when uploading. Sorry about that. I meant that, these doesn’t hold: alpha (x)<alpha (y), x and y in Q(sqrt(2)). But the order doesn’t hold anymore. But one could still find an order relation for the results of alpha?
1. Bill says:
  
  January 24, 2021 at 1:51 pm
  
  I’m sorry. I’m still not sure what you are asking. Are you asking if alpha can be used to define an order?
Diego says:

January 27, 2021 at 4:48 am

Sorry, I was very unclear. ” Alpha doesn’t preserve the order structure of Q(sqrt(2)) for the relation >”. Can I explain it in the following way?: -Because the relation > doesn’t hold anymore after alpha is applied to Q(sqrt(2)). Furthermore, I think you explained this in the youtube video, that alpha doesn’t preserve the order, doesn’t necessarily mean that a new relation can’t be found to define a new order for Q(sqrt(2)) for alpha.
Actually it turns out, I don’t know how to you call the set of elements that result from the map alpha? alpha (Q(sqrt(2))?
Thank you much.

Comments are closed.