The supremum and infimum of a bounded set of real numbers have many interesting properties
Study Help for Baby Rudin, Part 1.4

The Completeness Axiom for the real number system is intimately tied to the concept of the supremum of a set of real numbers which is bounded above.
Therefore, we should strive to understand the fundamental properties of the supremum. These properties of the supremum include the ones we discussed in the preceding article. In that article, “Least Upper Bound (Supremum) in an Ordered Set” (Study Help for Baby Rudin, Part 1.3), the supremum was defined and important examples were considered.
Here is the definition of the supremum of a set (a.k.a. least upper bound). For this article, we leave the definitions of ordered set and bounded above unstated.
Definition: Assume that is an ordered set and that
. Also assume that
is bounded above. An element
is the supremum (least upper bound) of
if the following two conditions are true.
is an upper bound of
. This means that if
, then
.
- If
, then
is not an upper bound of
. In other words, if
, then
such that
.
In this situation, we write .
There is an analogous definition of the infimum of a set (a.k.a. greatest lower bound). We state it for the record here.
Definition: Assume that is an ordered set and that
. Also assume that
is bounded below. An element
is the infimum (greatest lower bound) of
if the following two conditions are true.
is a lower bound of
. This means that if
, then
.
- If
, then
is not a lower bound of
. In other words, if
, then
such that
.
In this situation, we write .
The importance of the supremum and infimum to other results in Real Analysis, such as the Mean Value Theorem, is emphasized in the article “Deconstructing the Mean Value Theorem, Part 2”.
Fundamental Properties of the Supremum and Infimum
Some fundamental properties of the supremum and infimum include the facts that
and
. Here, as usual,
is the closed interval from
to
(containing the endpoints), and
is the open interval from
to
(not containing the endpoints).
To understand the proofs of these facts about the supremum, I’d recommend watching my video on the properties of the supremum, based on the previous article “Least Upper Bound (Supremum) in an Ordered Set”. I’m pretty happy with the way this video turned out. I think you’ll like it. The last example in the video is especially interesting and fun to visualize.
Based on the basic examples involving intervals above, we note that the supremum and the infimum of a set may or may not be an element of the set itself. This is very important to remember!
The Least Upper Bound Property (Completeness Property) and the First Tricky Proof of a Theorem in Baby Rudin
Part of the purpose of this article is to help you understand the first tricky proof of a theorem in Baby Rudin. This is not the first tricky argument in Baby Rudin, however. Indeed, I covered the first tricky argument in Baby Rudin near the end of the article “Baby Rudin: Let Me Help You Understand It” (Study Help for Baby Rudin, Part 1.1). A brief summary of that article is given in this short video:
The Completeness Axiom mentioned at the beginning of this article is the assumption that the field of real numbers satisfies the least upper bound property. But what is this property?
Definition: We say that an ordered set has the least upper bound property if the following implication is true. If
,
, and
is bounded above, then
exists in
.
The ordered field of rational numbers does not have the least upper bound property, as we saw in “Baby Rudin: Let Me Help You Understand It” (Study Help for Baby Rudin, Part 1.1).
As you might expect, there is an analogous greatest lower bound property.
Definition: We say that an ordered set has the greatest lower bound property if the following implication is true. If
,
, and
is bounded below, then
exists in
.
Though these might seem like distinct definitions, the first theorem in Baby Rudin, which is labeled Theorem 1.11 on page 5, shows that they are equivalent.
Baby Rudin Theorem 1.11: Ordered Sets with the Least Upper Bound Property Also Have the Greatest Lower Bound Property
Here is the statement of Theorem 1.11, which states more than the preceding heading implies.
Theorem 1.11 (page 5 of Baby Rudin, 3rd Edition): Suppose is an ordered set with the least upper bound property,
,
, and
is bounded below. Let
be the set of all lower bounds of
. Then
exists in
and
. In particular,
exists in
.
To grow as a mathematician, you should strive to first prove this on your own. It is tricky. It might take you a number of hours, especially if this is new for you.
But don’t give up! Keep trying!
Sleep on it if you need to do so. That is a great way to refresh your heart and mind. As a Christian, I also quiet my mind through biblically-grounded prayer to what I believe is the one true God.
Breaking Down My Thought Process
Now I will work through my thought process with a goal of writing a proof. After I am done showing my thought process, I will write a polished proof. I’m sure it will be different than the proof found in Baby Rudin. But it will also be instructive to compare the proofs.
Givens
I often start by writing down what I know (what I’m assuming is true from the theorem statement). Using shorthand notation and set-builder notation, I can write the “givens” (“assumptions” or “premises”) in the theorem statement as follows.
is an O.S. with the L.U.B. prop. (make sure you correctly determine what the abbreviations mean).
is bdd. below (bdd. is a somewhat standard abbreviation for “bounded”).
- Define
. In other words,
is defined to be the set of lower bounds of
. It is nonempty because
is assumed to be bounded below.
Must Shows
Now I write down what I must show (“conclusions”). There are really two things to show.
exists in
, and
, which clearly implies that
exists in
.
The Greek letter in the theorem statement is just shorthand notation.
Connecting the premises to the conclusions
I have just done the (relatively) “easy” part. I have written down what I am assuming and what I must show. Now comes the hard part: connecting the premises to the conclusions. To be a bit more precise: showing the conclusions logically follow from the premises.
What are my tools to complete this task? My tools are previous definitions, previous theorems (facts), and the rules and methods of logical deduction (deductive reasoning).
In this case, I don’t have any previous theorems, so I am restricted to using the other two tools. First off, if I am going to prove that exists in
, I’m going to have to “find” it or “construct” it.
Based on the fact that is assumed to have the L.U.B. prop., it seems that this “finding” or “constructing” will happen in an abstract way. In other words, I will probably just need to invoke the L.U.B. property.
Showing the Supremum of 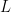 Exists in
Exists in 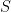
But how do I do this? Based on the definition of the L.U.B. prop., it looks like I need to show that is bounded above. I should also note that
. Why? As mentioned above, the assumptions in the theorem include the fact that
is bounded below in
. Therefore,
such that
. But this means
so
.
But is also nonempty! And, clearly, every element of
is an upper bound of
. Therefore
is bounded above. Since
has the least upper bound property, we logically conclude that
exists in
. Call it
.
Showing the Infimum of 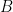 Exists in
Exists in 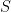 (and Equals the Supremum of
(and Equals the Supremum of 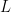 )
)
To prove that , we must use the definition of the infimum above.
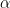 is a Lower Bound of
is a Lower Bound of 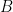
To show that is a lower bound of
, we must show that
. Towards this end, let
be given (or, “be arbitrary”).
But now we must be extremely careful! It is tempting to think that since
is the set of all lower bounds of
. However, this would be a faulty argument! Why? Because we cannot assume that
! For example, recall that
.
This call to be careful has extreme importance if you want to be a mathematician (or even to use advanced mathematics). You could lose your reputation, and possibly your job, if you are not careful!
Of course, everyone makes mistakes. The important things are to be honest about it when you do make mistakes, and to strive to fix your mistakes. It is also helpful to share your work with your colleagues before you present it to your boss.
Argument by Contradiction
So what should we do? It is probably worthwhile to explore whether an argument by contradiction (indirect proof) might be helpful.
Towards this end, assume to the contrary that . But since
, this means that
is not an upper bound of
. But this is impossible! By definition,
is the set of all lower bounds of
, which means
must be an upper bound of
.
Therefore, our assumption must be incorrect and we can correctly conclude that . Since
was arbitrary, we can now say that
. In other words,
is a lower bound of
.
Note that, by definition of as the set of all lower bounds of
, we can now conclude that
. However, we could not assume this as part of our proof. It must be proved if we are to use it.
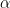 is the Greatest Lower Bound of
is the Greatest Lower Bound of 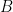
Finally, we must show that is the greatest lower bound of
. One way to do this is to prove the truth of the logical contrapositive of part (2) of the definition of the infimum. Part (2) says (switching “B” for “E“): if
, then
is not a lower bound of
. The contrapositive of this implication is: if
is a lower bound of of
, then
.
But this is easy to do, based on what we’ve done so far. For if is a lower bound of
, then
by definition of
. But
, which means that
is an upper bound of
and therefore
.
That does it! All this proves that . In particular,
exists in
so that
has the greatest lower bound property (G.L.B. prop.).
But, this is not a very “polished” argument/proof. For one thing, it is much too long!
A Polished Proof
For a “nice” and “polished” proof, I need to take my reasoning from above and cut out everything that is “unnecessary” (such as comments like “we must show”).
In addition, I should strive for “elegance”. Of course, there is not a unique way to do this. What does it mean for an argument to be “elegant”? In addition, it might not be clear what is “necessary” and what is “unnecessary”.
Answering these questions and writing a polished, but valid (and convincing), proof are matters of both experience and skill gained over time. Probably nobody is perfect at it (what does perfection mean here anyway?). It is something we can all grow in (though many people think Rudin is “close” to “perfect”).
Here’s my stab at it. The steps are:
1. Prove has a supremum in
,
2. Show the supremum of is the infimum of
by showing: i)
is a lower bound of
and ii) any other lower bound of
is less than or equal to
.
Proof:
The set of all lower bounds of
is nonempty and bounded above, since
is nonempty and bounded below. Since
satisfies the least upper bound property,
exists in
.
Let and suppose
. Then
is not an upper bound of
, contradicting the fact that
is the set of all lower bounds of
. Therefore,
. In other words,
is a lower bound of
.
If is a lower bound of
, then
. But since
, we conclude that
. In other words,
is the greatest lower bound of
.
Thus, and
exists in
.
The Proof in Baby Rudin
One main difference in the proof in Baby Rudin is stylistic: the same things are proved in different ways. Another difference is the fact that Rudin proves as part of his proof, and as I concluded in my “thought process” further above, but did not use in my proof.
Rudin’s Proof:
Since is bounded below,
. Since
consists of exactly those
which satisfy the inequality
, we see that every
is an upper bound of
.
Thus, is bounded above. Our hypothesis about
implies therefore that
has a supremum in
, call it
(so
).
If , then
is not an upper bound of
, hence
. It follows that
. Thus,
.
If , then
, since
is an upper bound of
.
We have shown that but
if
. In other words,
is a lower bound of
, but
is not if
. This means that
.
Other Fundamental Properties of the Supremum and Infimum
There are many other fundamental properties of the supremum and infimum that can be described. I will list some of them here and prove a couple of these. You should take the time to think about these intuitively with examples and pictures, and prove the ones that I do not take the time to prove here as fundamental exercises in Real Analysis.
Properties:
- (Exercise #5 in Chapter 1 of Baby Rudin) Reflection Property: Let
be a nonempty set of real numbers which is bounded below. Let
. Then
exists and
(stated another way,
.)
- Subset Properties: If
is a nonempty set of real numbers which is bounded above and
, then
exists and
. Likewise, if
is bounded below, then
exists and
.
- Inequality Relation: Let
and
be nonempty bounded (both above and below) sets of real numbers. If
, then
.
- Additive and Multiplicative Properties: Suppose
and
are nonempty sets of real numbers which are bounded above and suppose
. Let
and
. Then
and
exist in
. Moreover, i)
, and ii)
. Analogous facts about
and
are true when
and
are bounded below.
- Another Multiplicative Property: If
is a nonempty set of real numbers which is bounded above and
, then
exists in
and
. An analogous fact about
is true when
and
is bounded below.
- Finite Set Property: Let
be a nonempty finite set of real numbers, say
such that, WLOG,
. Then
and
.
- Definitional Property: Suppose
is a nonempty set of real numbers which is bounded above. If
, then
such that
. Likewise, if
is bounded above and
, then
such that
.
- Infinite Set Condition: Suppose
is a nonempty set of real numbers which is bounded above and suppose that
. Suppose further that
and that
Then
is an infinite set. If
is bounded below and
, then
is an infinite set.
- Union Property: Suppose
and
are nonempty and bounded (both above and below) in
. Then
and
.
A Couple Proofs
I will prove parts of properties 4 and 8. I leave the rest to you as exercises. Do them all!
First I will prove the part of property 4 that says when
and
are nonempty and bounded above.
Proof of Part of Property 4
Since and
are nonempty and bounded above in
, we can say that
and
exist in
(i.e., they are real numbers). We claim that
is the least upper bound of the set
.
Let represent an arbitrary element of
. Then
since
is an upper bound of
and
since
is an upper bound of
. Using properties of inequalities on ordered fields, we can “add” these inequalities to conclude that
. Thus,
is an upper bound of
and
exists as a real number.
Now suppose that . Set
and consider the numbers
and
. Also note that
.
Since and
, it follows that
is not an upper bound of
and
is not an upper bound of
. But this means there exist
and
such that
and
.
But then and also (by “adding” inequalities again),
. In other words,
is not an upper bound of
.
This means is the least upper bound of
. In other words,
, as desired.
Finally, I will prove that if is a nonempty set of real numbers which is bounded above and
. And if we suppose further that
and that
Then
is an infinite set.
Proof of Part of Property 8
This is an argument by contradiction.
Let be given. Suppose to the contrary that
is a finite set. Then, without loss of generality (WLOG), we may assume
for some natural number
, where
.
Since and
, we can say that
as well. Therefore, once again because
, we can say that
.
But this means is not an upper bound of
! In other words, there exists
such that
. But this would mean that
, which is impossible because
was not in the list of numbers assumed to equal
.
Therefore, our original assumption that was a finite set must be false. That is to say,
is an infinite set.
Make sure to take note of the relationship between properties 6 and 8!
