Existence of nth Roots of Positive Reals

The Completeness Axiom helps us prove the existence of nth roots of positive real numbers, but the proof is quite challenging.

Real Analysis Study Help for Baby Rudin, Part 1.6

The existence of nth roots, including the square root of two, is ultimately based on the continuity of power functions with positive integer exponents. — Ultimately, the continuity of $f(x)=x^{2}$ at $x=\sqrt{2}$ allows us to prove the existence of $\sqrt{2}$ . Later, the argument is based on the Intermediate Value Theorem. In this article, the argument is based on inequalities and the Completeness Axiom.

Ultimately, the continuity of $f(x)=x^{2}$ at $x=\sqrt{2}$ allows us to prove the existence of $\sqrt{2}$ . Later, the argument is based on the Intermediate Value Theorem. In this article, the argument is based on inequalities and the Completeness Axiom.

Everything in Real Analysis is built upon the foundational fact that the set of real numbers forms the unique complete ordered field. The completeness of 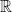$\Bbb{R}$ is the key factor that allows us to prove many fundamental facts that are taken for granted in pre-university education, including even in basic arithmetic.

For example, the Completeness Axiom allows us to prove, for any positive real number $x$ , the existence of nth roots of $x$ , where $n$ can be any positive integer ( $n\in \Bbb{Z}^{+}=\Bbb{N}$ ).

A real number $y$ is an nth root of $x$ if $y^{n}=x$ . In this case, we write $y=\sqrt[n]{x}$ or $y=x^{1/n}$ . When $n=2$ , the first notation is simplified to $\sqrt{x}$ .

Some roots are easy to “find” (or “construct”). For example, $\sqrt[4]{81}=3$ since $3^{4}=81$ . As another example that’s a bit more challenging, $\sqrt[5]{\frac{1024}{243}}=\frac{4}{3}$ since $\left(\frac{4}{3}\right)^{5}=\frac{1024}{243}$ .

Other roots are not so clear. For example, what is $\sqrt{2}$ ? One problem here is that, even if we assume $\sqrt{2}$ exists, it is not a rational number. I prove a more general fact in this video:

Prove Square Roots of Non-Perfect Squares are Irrational

I also address the existence of the square root of two, using the Completeness Axiom, in the article “Does the Square Root of Two Exist?”.

This is sixth article on Real Analysis study help for Baby Rudin. In it, we take a look the proof of the more general existence (and uniqueness) theorem for roots of positive real numbers. This is Theorem 1.21 found on page 10 of the third edition of Baby Rudin. It is the longest and hardest proof in the main part of Chapter 1 (other than in the Appendix).

Existence of nth Roots Theorem in Baby Rudin

Here is the official statement of the theorem. I’m calling it “Existence of nth roots”, though uniqueness is a part of the statement. The uniqueness portion is trivial to prove compared to the existence portion.

Theorem (Existence of nth Roots): For every real $x>0$ and every integer $n>0$ , there is one and only one real $y$ such that $y^{n}=x$ .

It’s not stated, but of necessity, $y$ is positive.

In the case where $x<0$ , you may recall that real nth roots exist when $n$ is odd. For example, $\sqrt[3]{-8}=-2$ .

On the other hand, there exists no real number $y$ such that $y^{2}=-4$ . In other words, $\sqrt{-4}$ does not exist as a real number. Most of you probably already know that it is an imaginary number. In fact, the symbol $\sqrt{-4}$ is typically thought of as representing two imaginary numbers, typically written $\pm 2i$ , where $i^{2}=-1$ . This can be contrasted with the (inconsistent) fact that the symbol $\sqrt{4}$ is typically thought of as representing just one real number (the positive square root $\sqrt{4}=2$ rather than the negative square root $-\sqrt{4}=-2$ ).

Let’s move on to the proof now. When working to understand a long and difficult proof, it is best to start by getting a feel for the overall strategy of proof. This can be done by outlining the proof.

Outlining the Proof of the Existence of nth Roots from Baby Rudin

Rudin starts by addressing uniqueness. Again, this part is trivial. If $0<y_{1}<y_{2}$ , then $y_{1}^{n}<y_{2}^{n}$ , so there can be no more than one number whose $n^{th}$ power equals the given $x>0$ .

If you desire, you can prove that $0<y_{1}<y_{2}\implies y_{1}^{n}<y_{2}^{n}$ using mathematical induction. The fact that $\Bbb{R}$ is an ordered field is also necessary to use.

The next step of the proof is not so clear for a beginner. You might say it is the most ingenious part of the proof. Gaining intuition about what to do here is based on the experience of seeing many proofs similar to this one.

The goal is to define a nonempty set of real numbers that is bounded above and whose least upper bound (supremum) we think/know will be $\sqrt[n]{x}$ . One such set is $E=\left\{t\in \Bbb{R}\ |\ 0<t\mbox{ and } t^{n}<x\right\}$ (think about this!). This is the set that Rudin uses. The proof that $E$ is nonempty and bounded above is relatively short, though a bit tricky. I will leave it as an exercise for you, though I give hints about what to do at the end of this article.

By the Completeness Axiom, $y=\sup(E)$ exists as a real number. The rest of the proof is the hardest part. We must confirm that $y^{n}=x$ . This involves the use of various mathematical inequalities that, to the uninitiated, seem to be pulled out of a hat.

Our Outline of the Proof So Far

So far, our outline of the entire proof (of Theorem 1.21) takes the following form.

Prove uniqueness (the easiest part of the proof)
Define a set whose supremum will be the number we seek (the ingenious part of the proof)
Invoke the Completeness Axiom to say the supremum of the set exists (the part of the proof where completeness of $\Bbb{R}$ is used)
Prove this supremum is the nth root we seek (the hardest part of the overall proof of the existence of nth roots)

Outlining the Hardest Part of the Proof of the Existence of nth Roots

The proof that $y=\sup(E)=\sup\left\{t\in \Bbb{R}\ |\ 0<t\mbox{ and } t^{n}<x\right\}$ satisfies $y^{n}=x$ is an argument by contradiction.

In fact, as described by William Dunham in Chapter 4 about Archimedes and the area of a circle in “Journey Through Genius, The Great Theorems of Mathematics”, we could even call this proof a double reductio ad absurdum proof. We prove that $y^{n}=x$ by showing that both of the following assumptions lead to logical contradictions: 1) $y^{n}<x$ and 2) $y^{n}>x$ . The contradictions are based on the definition of the least upper bound (supremum) of a set.

If you read through the details in Baby Rudin (which we will get to shortly in this article), you will see that the assumption that $y^{n}<x$ allows us to construct a real number $h>0$ such that $y+h\in E$ (and $y+h>y$ ), contradicting the fact that $y$ is an upper bound of $E$ . On the other hand, the assumption that $y^{n}>x$ allows us to construct a real number $k>0$ such that $y-k$ is an upper bound of $E$ (with $y-k<y$ ), contradicting the fact that $y$ is the least upper bound of $E$ .

These contradictions allow us to conclude that $y^{n}=x$ , making the proof complete.

The Outline of the Hardest Part of the Overall Proof

Our outline of the hardest part of the proof therefore takes the following form.

Assume $y^{n}<x$ and find $y<y+h\in E$ , contradicting the fact that $y$ is an upper bound of $E$ .
Assume $y^{n}>x$ and find an upper bound $y-k<y$ of $E$ , contradicting the fact that $y$ is the least upper bound of $E$ .
Use these two contradictions to conclude that $y^{n}=x$ .

However, to obtain these contradictions, we need a lemma whose conclusion is a mathematical inequality.

A Useful Inequality

Close to the middle of the overall proof of this theorem (Theorem 1.21) in Baby Rudin, a lemma is proved, though it is not labeled that way.

Lemma: If $0<a<b$ and $n\in \Bbb{N}$ , then $b^{n}-a^{n}<(b-a)nb^{n-1}$ .

Examples can help you believe this. For instance, if $a=2.3$ , $b=3.7$ , and $n=4$ , then $b^{n}-a^{n}=3.7^{4}-2.3^{4}=187.4161-27.9841=159.432$ while $(b-a)nb^{n-1}=1.4\cdot 4\cdot 3.7^{3}=283.6568$ .

Of course, examples are not proofs.

Proof of the Lemma

The actual proof of this lemma is based on a fundamental factorization fact that is worth memorizing. It is a generalization of the difference of two squares $b^{2}-a^{2}=(b-a)(b+a)$ and the difference of two cubes $b^{3}-a^{3}=(b-a)(b^{2}+ba+a^{2})$ . It is the difference of two nth powers:

$b^{n}-a^{n}=(b-a)(b^{n-1}+b^{n-2}a+b^{n-3}a^{2}+\cdots +b^{2}a^{n-3}+ba^{n-2}+a^{n-1})$ .

This factorization can be checked just by multiplication. Multiply $b$ by each term in the factor on the right, then multiply $-a$ by each term in the factor on the right, then combine “like terms” and simplify using cancellation.

It can also be proved using induction.

When $0<a<b$ , the truth of the lemma now follows from the following:

$b^{n-1}+b^{n-2}a+b^{n-3}a^{2}+\cdots +b^{2}a^{n-3}+ba^{n-2}+a^{n-1}$

$<b^{n-1}+b^{n-2}\cdot b+\cdots+b\cdot b^{n-2}+b^{n-1}=\underbrace{b^{n-1}+b^{n-1}+\cdots +b^{n-1}}_{n \text{ terms}}=nb^{n-1}$

Details of the Hardest Part of the Proof of the Existence of nth Roots

Now let’s dive even deeper into details. In this section we tackle the hardest part. How do we use the lemma to obtain the desired contradictions to the assumptions that $y^{n}<x$ and $y^{n}>x$ ? We take them one by one.

The kind of work we are about to do here is the “heart” of the “methods” of Real Analysis. It is impossible to become a good pure mathematical analyst without learning how to work through, and to gain intuition about, these kinds of details.

Assumption 1: 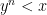$y^{n}<x$

First, assume that $y^{n}<x$ so that $x-y^{n}>0$ (remember this last inequality for later). Based on your past experience in a Calculus course, you should recognize $y^{n}$ to be a continuous function of $y$ (if you think of $y$ as a variable). Intuitively, but vaguely, close inputs lead to close outputs. Still intuitively but a bit more precisely, we can make the outputs as close as we like by taking the inputs to be sufficiently close to each other.

Because of this, it should make sense that, if $h>0$ is sufficiently small, we should be able to conclude that $(y+h)^{n}<x$ as well, which will imply that $y<y+h\in E$ , contradicting $y=\sup(E)$ . But how small is “sufficiently small”?

“Scratchwork” (the Problem-Solving Part of Proof Construction)

Based on the lemma above, we can write $(y+h)^{n}-y^{n}<((y+h)-y)n(y+h)^{n-1}=hn(y+h)^{n-1}$ . Since $(y+h)^{n}-y^{n}<x-y^{n}$ is equivalent to $(y+h)^{n}<x$ , our goal is to choose $h>0$ to be so small that $hn(y+h)^{n-1}<x-y^{n}$ .

If, without loss of generality, we choose $h<1$ as well, the truth of the inequality $hn(y+h)^{n-1}<x-y^{n}$ will follow from the truth of the inequality $hn(y+1)^{n-1}<x-y^{n}$ . But the inequality $hn(y+1)^{n-1}<x-y^{n}$ is equivalent to the inequality $h<\frac{x-y^{n}}{n(y+1)^{n-1}}$ (note that we are not dividing by zero). And, since $\frac{x-y^{n}}{n(y+1)^{n-1}}>0$ , we can certainly choose such a number $h$ .

Now let’s write out a formal proof that the assumption that $y^{n}<x$ leads to a contradiction. In essence, we have to reverse our scratch work so that the logical steps are in the right order.

Proof that Assumption 1 Leads to a Contradiction:

Suppose $y^{n}<x$ so that $x-y^{n}>0$ and $\frac{x-y^{n}}{n(y+1)^{n-1}}>0$ (note that we are not dividing by zero since $y>0>-1$ so $y+1>0$ ). By a corollary of the Archimedean Property (see the end of the article “The Archimedean Property“), we can choose a real number $h>0$ such that $h<\min\left\{1,\frac{x-y^{n}}{n(y+1)^{n-1}}\right\}$ (this is just a fancy way of saying that $h<1$ and $h<\frac{x-y^{n}}{n(y+1)^{n-1}}$ ).

The fact that $h<1$ implies that $y+h<y+1$ , while the fact that $h<\frac{x-y^{n}}{n(y+1)^{n-1}}$ implies that $hn(y+1)^{n-1}<x-y^{n}$ .

Then, by the lemma above, $(y+h)^{n}-y^{n}<((y+h)-y)n(y+h)^{n-1}=hn(y+h)^{n-1}<hn(y+1)^{n-1}<x-y^{n}.$ This means that $(y+h)^{n}<x$ so that $y<y+h\in E$ , contradicting the fact that $y=\sup(E)$ is an upper bound of $E=\left\{t\in \Bbb{R}\ |\ 0<t\mbox{ and } t^{n}<x\right\}$ .

Q.E.D.

Assumption 2: 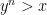$y^{n}>x$

Next, assume that $y^{n}>x$ so that $y^{n}-x>0$ (remember this last inequality for later). Again, $y^{n}$ is a continuous function of $y$ . Because of this, it should make sense that, if $k>0$ is sufficiently small, we should be able to conclude that $(y-k)^{n}>x$ as well, which will ultimately imply (after some other work) that $y-k$ is an upper bound of $E$ (and $y-k<y$ ), contradicting $y=\sup(E)$ . But again, how small is “sufficiently small”?

Scratchwork

Based on the lemma above, we can write $y^{n}-(y-k)^{n}<(y-(y-k))ny^{n-1}=kny^{n-1}$ . Since $y^{n}-(y-k)^{n}<y^{n}-x$ is equivalent to $(y-k)^{n}>x$ , our goal is to choose $k>0$ to be so small that $kny^{n-1}<y^{n}-x$ .

This last inequality is equivalent to choosing $k>0$ so that $k<\frac{y^{n}-x}{ny^{n-1}}$ . Note that we are not dividing by zero here because $n>0$ and $y>0$ . In fact, in the proof, we will actually choose $k=\frac{y^{n}-x}{ny^{n-1}}>0$ and show that $t\geq y-k$ implies that $t\not\in E$ . Doing this is equivalent to proving that if $t\in E$ , then $t<y-k$ . This, in turn, means that $y-k$ is an upper bound of $E$ (with $y-k<y$ ), leading to a contradiction that $y=\sup(E)$ is the least upper bound of $E$ .

Here is the formal proof.

Proof that Assumption 2 Leads to a Contradiction:

Suppose $y^{n}>x$ so that $y^{n}-x>0$ and $\frac{y^{n}-x}{ny^{n-1}}>0$ (note that we are not dividing by zero since $y>0$ and $n>0$ ). Choose $k=\frac{y^{n}-x}{ny^{n-1}}>0$ and note that $k<\frac{y^{n}}{ny^{n-1}}=\frac{y}{n}\leq y$ since $n\geq 1$ .

Then, if $t\geq y-k$ , we can say that $t^{n}\geq (y-k)^{n}$ and $-t^{n}\leq -(y-k)^{n}$ . This implies that $y^{n}-t^{n}\leq y^{n}-(y-k)^{n}$ .

By the lemma above, we can then conclude that $y^{n}-t^{n}<kny^{n-1}=\frac{y^{n}-x}{ny^{n-1}}\cdot ny^{n-1}=y^{n}-x$ . Hence, $-t^{n}<-x$ and $t^{n}>x$ . Therefore, $t\not\in E$ , implying that $y-k$ is an upper bound of $E$ .

But $y-k<y=\sup(E)$ , contradicting the fact that $y=\sup(E)$ is the least upper bound of $E$ .

Q.E.D.

Therefore, since both of these assumptions lead to contradiction, we may conclude that $y^{n}=x$ (we are also using the Law of Trichotomy here, which is related to the concept of a total order).

Q.E.D. for Theorem 1.21 (with some details missing)

Have We Missed Any Details in the Proof of the Existence of nth Roots?

The proof of Theorem 1.21 is actually not quite complete. We did not fill in the details of showing that $E=\left\{t\in \Bbb{R}\ |\ 0<t\mbox{ and } t^{n}<x\right\}$ is nonempty and bounded above. We leave those details to you. Of course, the details can also be found in Baby Rudin.

If you would like hints about how to prove it on your own without looking at Baby Rudin, here are a couple. 1) To prove that $E\not=\emptyset$ , show that $\frac{x}{1+x}\in E$ . 2) To prove that $E$ is bounded above, show that $1+x$ is an upper bound of $E$ . Now you figure out the details of how to prove these “lemmas”.