Linear Transformations in Two Dimensions

Visual Linear Algebra Online, Section 1.4

The set $A$ (red) is the butterfly curve and $T(A)$ (blue) is its image under a linear transformation that reflects across the line $y=x$ .

We have already alluded to the idea of linear transformations in two dimensions at various points in the first three sections. One example we encountered, in Section 1.1, “Points, Coordinates, and Graphs in Two Dimensions”, consisted of a system of linear equations that transformed rectangular coordinates to slanted coordinates.

Other examples of a linear transformations in two dimensions arose in the exercises of that section. There, for example, a system of linear equations transformed rectangular coordinates to rotated coordinates.

We also saw rotations arise as ways to visualize the process of elimination in Section 1.3, “Systems of Linear Equations in Two Dimensions”. However, because the rotations considered in that section are not about the origin, it turns out that those transformations are not linear. The reasons for that will be explored in this section.

Linear Functions and Linear Transformations

Linear Functions in Calculus

In calculus and its prerequisite subjects, a linear function $f$ is one whose graph, in rectangular coordinates, is a straight line. This is equivalent to the formula for the function being of the form $y=f(x)=mx+b$ for some constants $m$ and $b$ . The constant $m$ is called the slope of the line. And the constant $b$ is called the $y$ -intercept of the line. Take note of the fact that, in the equation $y=mx+b$ , both $y$ and $x$ appear to the first power.

Linear Transformations as Mappings and Vector Fields

This definition of a linear function is simple, but in linear algebra we choose to define a linear function differently. We also tend to give it a different name — a linear transformation.

The words “transformation” and “function” are basically synonyms in mathematics. However, the word “transformation” has a connotation to its meaning that is a bit more geometric/visual.

We are especially interested in visualizing linear transformations in two ways, described below. These descriptions introduce a bit more terminology that we will explore in the examples to follow.

Linear transformations are linear mappings (or linear maps, for short), which take a given set of points and “send” or “map” these points to another set of points.
Linear transformations are linear vector fields which take a given set of points and “attach” vectors to them.

We now commence with our exploration through examples.

Examples of Linear Transformations

Within each example of this section, we start by describing transformations geometrically. We also consider what makes each transformation linear or not. Most of these are examples of linear transformations in two dimensions.

We will find it helpful to use a special symbol for the two-dimensional rectangular (Cartesian) coordinate plane. The symbol we use is standard. It is ${\Bbb R}^{2}$ .

We also use the standard notation $f:A\longrightarrow B$ for a function (transformation) whose domain is $A$ and whose codomain is $B$ .

Example 1: Reflection about the horizontal axis

Define a transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ geometrically in the following way. Map a point with rectangular coordinates $(x,y)$ to a point that is its reflection across the horizontal axis.

In other words, if the input of $T$ has rectangular coordinates $(x,y)$ , the output will have rectangular coordinates $(x,-y)$ . This can be written in function notation as $T(x,y)=(x,-y)$ (which is a simplification of $T((x,y))=(x,-y)$ ). We will also write it with “maps to” notation $(x,y)\mapsto (x,-y)$ , or $(x,y)\xrightarrow{T} (x,-y)$ .

If we let $u$ be the first coordinate/component of the output and let $v$ be the second coordinate/component of the output $(u,v)=T(x,y)$ , this transformation can also be written as the following system of linear equations.

$\begin{cases}\begin{array}{rcl} u & = & x \\ v & = & -y \end{array} \end{cases}$

Visualizing the Mapping

This transformation can be visualized as shown below.

A visual for the transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ which maps a point $(x,y)$ to its reflection across the horizontal axis $(x,-y)$ . The mapping has this geometric effect for all points in the plane. This also means that points that start out below the horizontal axis get mapped to points above the horizontal axis. Points exactly on the horizontal axis get mapped to themselves.

A visual for the transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ which maps a point $(x,y)$ to its reflection across the horizontal axis $(x,-y)$ . The mapping has this geometric effect for all points in the plane. This also means that points that start out below the horizontal axis get mapped to points above the horizontal axis. Points exactly on the horizontal axis get mapped to themselves.

Alternatively, via the natural association between points and vectors discussed in Section 1.2 “Vectors in Two Dimensions”, we can view this as a transformation of vectors. This can be written $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} x \\ -y \end{array}\right)$ , or as $\left(\begin{array}{c} x \\ y \end{array}\right)\mapsto \left(\begin{array}{c} x \\ -y \end{array}\right)$ . It can be visualized as shown below.

The same reflection across the horizontal axis, but conceptualized as a transformation of vectors rather than of points.

The Image of a Set of Points

Suppose we are given a set of points $A\subseteq {\Bbb R}^{2}$ in the domain of $T$ . It is often important to determine the set of all outputs of $T$ as the inputs vary over this set.

This set of outputs is called the image of $A$ under $T$ , and is denoted by $T(A)$ . It is defined by the equation $T(A)=\{T(x,y)\, |\, (x,y)\in A\}$ . Read this as “the set of all points $T(x,y)$ as the points $(x,y)$ vary over the set $A$ ” (the symbol $\in$ means “is an element of” or “is in”).

For example, suppose $A=\{(x,y)\, |\, -10\leq x-4y\leq 0\mbox{ and } 0\leq 3x-2y\leq 10\}$ . With a bit of algebra work, you will see that $A$ is the parallelogram bounded by the lines $y=\frac{1}{4}x$ , $y=\frac{1}{4}x+\frac{5}{2},$ $y=\frac{3}{2}x$ , and $y=\frac{3}{2}x-5$ .

An animation showing $A$ being transformed into its image $T(A)$ is shown below. The quantity $\lambda$ is just an “animation parameter” that has no meaning. It is just a tool to help us visualize the reflection.

The image $T(A)$ of a parallelogram $A$ under a reflection across the horizontal axis is another parallelogram.

The image $T(A)$ of a parallelogram $A$ under a reflection across the horizontal axis is another parallelogram.

While it is useful and relatively simple to consider images of parallelograms, we need not be constrained by them. We can consider the image of a more complicated set, such as the “butterfly curve”. Once again, $\lambda$ is just an animation parameter with no meaning.

The set of points $A$ (red) is the ‘butterfly curve’. Its image $T(A)$ is the blue butterfly curve that is upside-down.

From these examples, you can start to get an inkling of how linear algebra is useful for computer graphics!

What Makes the Reflection Linear?

But why is this reflection a linear transformation? For one thing, in its formula, the output contains the input variables only to the first power: $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} x \\ -y \end{array}\right)$ .

A more important (related) reason is this: $T(s{\bf u}+t{\bf v})=sT({\bf u})+tT({\bf v})$ for any vectors ${\bf u},{\bf v}\in {\Bbb R}^{2}$ and any scalars (numbers) $s,t \in {\Bbb R}$ (just a plain ${\Bbb R}$ , with no “2” in its “exponent”, is the symbol for the set of all real numbers).

To see why this is true, let ${\bf u}=\left(\begin{array}{c} x_{1} \\ y_{1} \end{array}\right)$ and ${\bf v}=\left(\begin{array}{c} x_{2} \\ y_{2} \end{array}\right)$ . Then, by the definition of vector addition and scalar multiplication, $s{\bf u}+t{\bf v}=\left(\begin{array}{c} sx_{1}+tx_{2} \\ sy_{1}+ty_{2}\end{array}\right)$ .

Then

$T(s{\bf u}+t{\bf v})=T\left(\begin{array}{c} sx_{1}+tx_{2} \\ sy_{1}+ty_{2}\end{array}\right)=\left(\begin{array}{c} sx_{1}+tx_{2} \\ -(sy_{1}+ty_{2})\end{array}\right)=\left(\begin{array}{c} sx_{1}+tx_{2} \\ -sy_{1}-ty_{2}\end{array}\right)$ .

On the other hand,

$sT({\bf u})+tT({\bf v})=sT\left(\begin{array}{c} x_{1} \\ y_{1} \end{array}\right)+tT\left(\begin{array}{c} x_{2} \\ y_{2} \end{array}\right)$

$=s\left(\begin{array}{c} x_{1} \\ -y_{1} \end{array}\right)+t\left(\begin{array}{c} x_{2} \\ -y_{2} \end{array}\right)=\left(\begin{array}{c} sx_{1}+tx_{2} \\ -sy_{1}-ty_{2}\end{array}\right)$ .

Hence, $T(s{\bf u}+t{\bf v})=sT({\bf u})+tT({\bf v})$ for any vectors ${\bf u},{\bf v}\in {\Bbb R}^{2}$ and any scalars (numbers) $s,t \in {\Bbb R}$ .

What Makes This Work?

It is, in part, the first powers of $x$ and $y$ that allow for this computation to work out in the way that it does. Also, this computation works out because there are no constants that are being added (by themselves with no variable attached) in the formula for $T$ .

You should take the time to check that there are vectors ${\bf u}, {\bf v}\in {\Bbb R}^{2}$ and scalars $s,t\in {\Bbb R}$ such that $T(s{\bf u}+t{\bf v})\not=sT({\bf u})+tT({\bf v})$ (note the not equal to!) for the following two examples. You only have to come up with one example in each case to show the transformations are not linear!

$T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c}x^{2} \\ -y\end{array}\right)$ .
$T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c}x+1 \\ -y\end{array}\right)$ .

Now you might ask: why not allow linear transformations to include situations where constants are being added? The short answer is this. Defining a linear transformation purely by the property $T(s{\bf u}+t{\bf v})=sT({\bf u})+tT({\bf v})$ allows us to: both 1) state various properties more clearly and 2) generalize the idea of linearity to many other situations.

Example 2: Reflection about the line y = x

If you think carefully, you will see that the formula for $T$ is $T(x,y)=(y,x)$ (swap the coordinates). In “maps to” notation, we write $(x,y)\mapsto (y,x)$ or $(x,y)\xrightarrow{T} (y,x)$ . With vectors, we write $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} y \\ x \end{array}\right)$ (swap the components).

As a system of linear equations, $T$ is defined by

$\begin{cases}\begin{array}{rcl} u & = & y \\ v & = & x.\end{array}\end{cases}$

The figure below shows how the transformation acts on both the point $(x,y)$ and the vector $\left(\begin{array}{c} x \\ y \end{array}\right)$ . Note that the green dashed line $y=x$ is a perpendicular bisector of the black dashed line from $(x,y)$ to its image $T(x,y)=(y,x)$ .

Also, make sure you don’t get confused by the notation. For the image point $(y,x)$ , the value of $y$ is indeed its $x$ -coordinate (first coordinate) and vice versa.

*A visual for the transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ which maps a point $(x,y)$ to its reflection $(y,x)$ across the $45^{\circ}$ line $y=x$ .* In this picture, we see that $T(-2,5)=(5,-2)$ .

The Images of Sets of Points

We now consider the images of the parallelogram and the butterfly curve defined in Example 1.

Here is the relevant animation for the parallelogram $A=\{(x,y)\, |\, -10\leq x-4y\leq 0\mbox{ and } 0\leq 3x-2y\leq 10\}$ .

*The image $T(A)$ of a parallelogram $A$ under a reflection across the line $y=x$ is another parallelogram.*

*The image $T(A)$ of a parallelogram $A$ under a reflection across the line $y=x$ is another parallelogram.*

And here is the relevant animation for the butterfly curve.

*The set of points $A$ (red) is the ‘butterfly curve’. Its image $T(A)$ is the blue butterfly curve that is sideways.*

What Makes the Reflection Linear?

Once again, the key fact that makes this reflection linear is that $T(s{\bf u}+t{\bf v})=sT({\bf u})+tT({\bf v})$ for any vectors ${\bf u},{\bf v}\in {\Bbb R}^{2}$ and any scalars (numbers) $s,t \in {\Bbb R}$ . You should check this as an exercise.

We take the time to note that this condition is equivalent to the following two facts being true.

$T({\bf u}+{\bf v})=T({\bf u})+T({\bf v})$ for any vectors ${\bf u},{\bf v}\in {\Bbb R}^{2}$ , and
$T(s{\bf u})=sT({\bf u})$ for any vector ${\bf u}\in {\Bbb R}^{2}$ and any scalar $s\in {\Bbb R}$

We also remark that mathematical induction can be used to prove that, for an arbitrary collection of $n$ vectors and $n$ scalars,

$T(s_{1}{\bf u}_{1}+s_{2}{\bf u}_{2}+\cdots+s_{n}{\bf u}_{n})=s_{1}T({\bf u}_{1})+s_{2}T({\bf u}_{2})+\cdots+s_{n}T({\bf u}_{n})$ .

Using Sigma (summation) notation, this property can be written like this:

$T\left(\displaystyle\sum_{i=1}^{n}s_{i}{\bf u}_{i}\right)=\displaystyle\sum_{i=1}^{n}s_{i}T({\bf u}_{i})$ .

Once you know a given transformation is linear, you may use these equations any time you need it. These facts are all related and do have a name. Any of them can be called an operation-preserving property of a linear transformation.

Example 3: Expansion (Dilation) Away From the Origin

Define a transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ geometrically in the following way. Map the point $(x,y)$ to another point along the same ray from the origin, but twice as far from the origin.

This means the formula for $T$ can be written as $T(x,y)=(2x,2y)$ or $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} 2x \\ 2y \end{array}\right)$ .

As a system of linear equations, $T$ is defined by

$\begin{cases}\begin{array}{rcl} u & = & 2x \\ v & = & 2y.\end{array}\end{cases}$

The figure below shows the action of this transformation on a generic point/vector.

A visual for the transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ which maps a point/vector $(x,y)$ to the point/vector $(2x,2y)$ which is twice as far from the origin along the same ray from the origin.

The Images of Sets of Points

We again consider the images of the parallelogram and the butterfly curve defined in Example 1. First, an animation of for the parallelogram.

*The image $T(A)$ of a parallelogram $A$ under an expansion away from the origin by a factor of two.*

*The image $T(A)$ of a parallelogram $A$ under an expansion away from the origin by a factor of two.*

And here is the animation for the butterfly curve.

*The set of points $A$ (red) is the ‘butterfly curve’. Its image $T(A)$ is the blue butterfly curve that is twice as big.*

Take the time to check linearity. Check that $T(s{\bf u}+t{\bf v})=sT({\bf u})+tT({\bf v})$ for any vectors ${\bf u},{\bf v}\in {\Bbb R}^{2}$ and any scalars $s,t\in {\Bbb R}$ .

Example 4: Rotation About the Origin

Define a transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ geometrically in the following way. Map the point/vector $(x,y)$ to a point/vector that is a $90^{\circ}$ counterclockwise rotation about the origin.

The formula for this turns out to be $T(x,y)=(-y,x)$ or $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} -y \\ x \end{array}\right)$ .

As a system of linear equations, $T$ is defined by

$\begin{cases}\begin{array}{rcl} u & = & -y \\ v & = & x.\end{array}\end{cases}$

This is best shown with a picture.

The transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ which maps a point/vector $(x,y)$ to the point/vector $(-y,x)$ . This is a counterclockwise rotation of $90^{\circ}$ about the origin. In this picture, we see that $T(5,2)=(-2,5)$ .

The Images of Sets of Points

Here is an animation of the image of our parallelogram.

*The image $T(A)$ of a parallelogram $A$ under a rotation of 90 degrees counterclockwise about the origin.*

*The image $T(A)$ of a parallelogram $A$ under a rotation of 90 degrees counterclockwise about the origin.*

And here is an animation for the butterfly curve.

*The set of points $A$ (red) is the ‘butterfly curve’. Its image $T(A)$ is the blue butterfly curve that is rotated counterclockwise by 90 degrees about the origin.*

You should once again take the time to check linearity.

Example 5: Shear Transformation

Another kind of transformation that is linear is a “shear transformation”. One basic example of this type maps the horizontal vector $\left(\begin{array}{c} 1 \\ 0 \end{array}\right)$ to itself while mapping the vertical vector $\left(\begin{array}{c} 0 \\ 1 \end{array}\right)$ to $\left(\begin{array}{c} 1 \\ 1 \end{array}\right)$ .

It is important to imagine the geometric effect of this transformation on the vertical vector as “pushing” (“shearing”) the vector to the right so that it stays the same height but gets more and more slanted. It is also important to realize that similar behavior is going on below the horizontal axis, but in the leftward direction. This means the downward-pointing vertical vector $\left(\begin{array}{c} 0 \\ -1 \end{array}\right)$ gets mapped to $\left(\begin{array}{c} -1 \\ -1 \end{array}\right)$ .

The resulting formula for this turns out to be $T(x,y)=(x+y,y)$ or $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} x+y \\ y \end{array}\right)$ .

As a system of linear equations, $T$ is defined by

$\begin{cases}\begin{array}{rcl} u & = & x+y \\ v & = & y.\end{array}\end{cases}$

Checking the linearity (operation-preserving) condition is a tiny bit more work in this case. Take the time to do so before looking at the visuals below.

*The shearing transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ . An arbitrary point/vector $(x,y)$ gets mapped to $(x+y,y)$ .* This results in a rightward “pushing” when the point/vector is above the horizontal axis and a leftward “pushing” when it is below.

The Images of Sets of Points

The “pushing effect” is easier to see when we look at our old friends, the parallelogram and the butterfly curve.

*The image $T(A)$ of a parallelogram $A$ under a horizontal shear transformation. There is a rightward ‘pushing effect’ here because the parallelogram is above the horizontal axis.*

*The image $T(A)$ of a parallelogram $A$ under a horizontal shear transformation. There is a rightward ‘pushing effect’ here because the parallelogram is above the horizontal axis.*

The set of points $A$ (red) is the ‘butterfly curve’. Its image $T(A)$ is the blue butterfly curve that is a horizontal shear of the original curve. The ‘pushing effect’ is rightward above the horizontal axis and leftward below it.

**Example 6: Translation (a Nonlinear Transformation!)**

A geometric translation (shift) is certainly a simple transformation. For example, we could take all the points in the plane and shift them to the right by 3 units and upward by 2 units.

As a mapping $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ , the formula for this would be $T(x,y)=(x+3,y+2)$ or $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} x+3 \\ y+2 \end{array}\right)$ .

This certainly looks both simple and linear. However, according to our “new” definition of linearity, it is nonlinear. To see this, we only need to find one example of scalars $s,t\in {\Bbb R}$ and vectors ${\bf u},{\bf v}\in {\Bbb R}^{2}$ such that $T(s{\bf u}+t{\bf v})\not=sT({\bf u})+tT({\bf v})$ .

Probably any example you pick will be sufficient. For example, suppose $s=t=1$ , ${\bf u}=\left(\begin{array}{c}4 \\ 3\end{array}\right)$ , and ${\bf v}=\left(\begin{array}{c}2 \\ 5\end{array}\right)$ . Then

$T(s{\bf u}+t{\bf v})=T\left(\begin{array}{c} 6 \\ 8\end{array}\right)=\left(\begin{array}{c} 9 \\ 10\end{array}\right)$ .

On the other hand,

$sT({\bf u})+tT({\bf v})=T\left(\begin{array}{c} 4 \\ 3\end{array}\right)+T\left(\begin{array}{c} 2 \\ 5\end{array}\right)=\left(\begin{array}{c} 7 \\ 5\end{array}\right)+\left(\begin{array}{c} 5 \\ 7\end{array}\right)=\left(\begin{array}{c} 12 \\ 12\end{array}\right)$ .

We can still think about images of sets of points with such a transformation. In fact, for translations, this is relatively easy. But still, the larger point holds: this transformation is actually nonlinear.

**Example 7: Rotation About a Point that is Not the Origin (a Nonlinear Transformation!)**

A rotation of points about a given point that is not the origin is likewise a simple transformation that is nonlinear.

To find a formula for such a transformation, it is best to think in stages. For example, suppose we want to rotate points by $90^{\circ}$ counterclockwise about the point $(3,2)$ .

We could start by using a translation that maps $(3,2)$ to the origin. This mapping could be represented as $(x,y)\mapsto (x-3,y-2)$ .

Next, we could rotate the resulting points about the origin (see Example 4). This mapping is $(x,y)\mapsto (-y,x)$ .

Finally, translate the result back to be centered on the original point by using the mapping $(x,y)\mapsto (x+3,y+2)$ .

The composition of these three functions is the mapping we seek. In stages, it would be $(x,y)\mapsto (x-3,y-2)\mapsto (-(y-2),x-3)=(2-y,x-3)$

$\mapsto (2-y+3,x-3+2)=(-y+5,x-1)$ .

The $+5$ and the $-1$ in the formula $T(x,y)=(-y+5,x-1)$ conspire to make this a nonlinear transformation according to our new sense of linearity.

Example 8: Polar Coordinates (a “Strongly” Nonlinear Transformation)

Recall our brief discussion of polar coordinates at the end of Section 1.1, “Points, Coordinates, and Graphs in Two Dimensions”. The “conversion equations” from polar coordinates $(r,\theta)$ to rectangular coordinates $(x,y)$ are:

$\begin{cases}\begin{array}{rcl} x & = & r\cos(\theta) \\ y & = & r\sin(\theta). \end{array}\end{cases}$

This defines a transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ by the formula $\left(\begin{array}{c} x \\ y \end{array}\right)=T\left(\begin{array}{c} r \\ \theta \end{array}\right)=\left(\begin{array}{c} r\cos(\theta) \\ r\sin(\theta) \end{array}\right)$ .

It is important to realize in the last paragraph that the ${\Bbb R}^{2}$ on the left has rectangular coordinates that are labeled with the letters $r$ and $\theta$ while the ${\Bbb R}^{2}$ on the right has rectangular coordinates labeled with the letters $x$ and $y$ . This may seem like quite a strange thing to do, but it indeed is the best way to think about it.

It is interesting to watch the butterfly curve being transformed under this mapping. Keep in mind that it is most definitely a (strongly) nonlinear mapping, which makes its behavior more difficult to understand. Take note of how the butterfly is essentially being wrapped around the origin in a strange way. In fact, the larger the initial second $\theta$ -coordinate is, in absolute value, the larger the amount of wrapping in the final picture.

Also note how the axes get relabeled during the animation.

*The effect of the polar coordinate transformation on the butterfly curve. This is most definitely a nonlinear transformation.*

Example 9: Projection Onto the Horizontal Axis

For our final example of a transformation, we return to one that is linear. Its behavior, however, is somewhat “degenerate” in certain ways.

Define a transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ by mapping every point to a point on the horizontal $x$ -axis with the same $x$ -coordinate. The formula for $T$ is $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} x \\ 0 \end{array}\right)$ . It is easy to check that $T$ is linear.

Here is a picture of the effect of this linear transformation, called a “projection”, on an arbitrary point/vector. It is called this because the image point/vector is like a “shadow” of the original points/vector. In the present example, the “light source” that causes this shadow to be cast has “light rays” that come straight down/up perpendicular to the horizontal axis.

*The projection mapping $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ onto the horizontal axis. An arbitrary point/vector $(x,y)$ gets mapped to $(x,0)$ .*

The Images of Sets of Points

Here is an animation showing the geometric effect of this projection mapping on our parallelogram and the butterfly curve. Notice that both sets get “squashed” onto the $x$ -axis. This is the reason the mapping is “degenerate”.

The images of the parallelogram and butterfly curve under projection to the horizontal $x$ -axis.

Observations about the Examples

Some summary observations about these examples are in order.

Some linear transformations are “rigid” (isometries): they preserve distances and areas. Examples of this include rotations about the origin and reflections across lines through the origin fall in this category.
There are some nonlinear transformations that are also rigid. Translations, rotations about non-origin points, and reflections about lines that do not go through the origin fall in this category (we did not consider an example of the last type).
Some linear transformations are not rigid. Expansions (dilations) and projections do not preserve distances or areas. Shears do not preserve distances.
For “most” linear transformations from the plane to itself, the origin is the only point that gets mapped to the origin. This is true for all of our linear transformation examples except for the projection mapping. This is equivalent to “most” linear transformations $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ being one-to-one.
For “most” linear transformations from the plane to itself, every point is the image of some other point. This is true for all of our linear transformation examples except for the projection mapping. This is equivalent to “most” linear transformations $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ being onto.

The Examples Reimagined as Vector Fields

As mentioned earlier, there is another way that transformations like these can be visualized: as vector fields. Given a transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ , we imagine “attaching” the vector (arrow) $T(x,y)$ to be based at the point $(x,y)$ , for all points in the plane.

This perspective is of utmost importance in applying linear algebra to the study of differential equations. More on this topic to come in later sections of this text.

Examples 1 and 2

The formula for such a transformation as a vector field can be written in a suggestive form, with the input as a point and the output as a (column) vector. For Examples 1 and 2 above, the forms would be $T(x,y)=\left(\begin{array}{c} x \\ -y \end{array}\right)$ and $T(x,y)=\left(\begin{array}{c} y \\ x \end{array}\right)$ .

The vector field-graphs for these two examples are shown below. For formatting reasons, we are not able to label these plots with outputs as column vectors. The big dot at the origin for each graph represents the fact that $T(0,0)=\left(\begin{array}{c} 0 \\ 0 \end{array}\right)$ in each case. This is a “degenerate arrow” which has zero length and no well-defined direction.

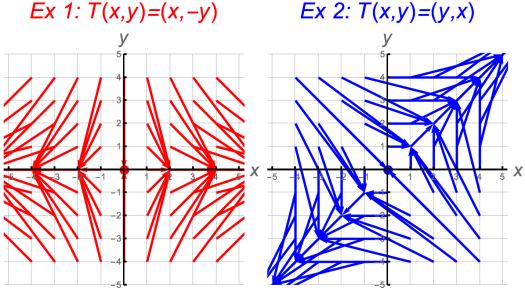
The linear transformations from Examples 1 and 2, visualized as vector fields. For any point $(x,y)$ , such as $(x,y)=(2,1)$ , the output is an arrow/vector based at that point. In the vector field on the left, this output is $\left(\begin{array}{c} 2 \\ -1\end{array}\right)$ . *In the vector field on the right, this output is $\left(\begin{array}{c} 1 \\ 2\end{array}\right)$ .*

The linear transformations from Examples 1 and 2, visualized as vector fields. For any point $(x,y)$ , such as $(x,y)=(2,1)$ , the output is an arrow/vector based at that point. In the vector field on the left, this output is $\left(\begin{array}{c} 2 \\ -1\end{array}\right)$ . *In the vector field on the right, this output is $\left(\begin{array}{c} 1 \\ 2\end{array}\right)$ .*

Examples 3 and 4

For Examples 3 and 4, the formulas are $T(x,y)=\left(\begin{array}{c} 2x \\ 2y \end{array}\right)$ and $T(x,y)=\left(\begin{array}{c} -y \\ x \end{array}\right)$ .

The plots for Examples 3 and 4 are shown below. The expansion one (example 3) is a bit tough to see because the arrows lie on top of each other and get so long. Once again, the big dot at the origin represents the fact that $T(0,0)=\left(\begin{array}{c} 0 \\ 0 \end{array}\right)$ .

The linear transformations from Examples 3 and 4, visualized as vector fields. For any point $(x,y)$ , such as $(x,y)=(2,1)$ , the output is an arrow/vector based at that point. In the vector field on the left, this output is $\left(\begin{array}{c} 4 \\ 2\end{array}\right)$ . In the vector field on the right, this output is $\left(\begin{array}{c} -1 \\ 2\end{array}\right)$ .

The linear transformations from Examples 3 and 4, visualized as vector fields. For any point $(x,y)$ , such as $(x,y)=(2,1)$ , the output is an arrow/vector based at that point. In the vector field on the left, this output is $\left(\begin{array}{c} 4 \\ 2\end{array}\right)$ . In the vector field on the right, this output is $\left(\begin{array}{c} -1 \\ 2\end{array}\right)$ .

Examples 5 and 6

For Examples 5 and 6, the formulas are $T(x,y)=\left(\begin{array}{c} x+y \\ y \end{array}\right)$ and $T(x,y)=\left(\begin{array}{c} x+3 \\ y+2 \end{array}\right)$ .

The plots for Examples 5 and 6 are shown below. Note that the “big dot” for the second one is not at the origin. This is related to the fact that example 6 is a nonlinear transformation.

The transformations from Examples 5 and 6, visualized as vector fields. For any point $(x,y)$ , such as $(x,y)=(2,1)$ , the output is an arrow/vector based at that point. In the vector field on the left, this output is $\left(\begin{array}{c} 3 \\ 1 \end{array}\right)$ . In the vector field on the right, this output is $\left(\begin{array}{c} 5 \\ 3\end{array}\right)$ .

The transformations from Examples 5 and 6, visualized as vector fields. For any point $(x,y)$ , such as $(x,y)=(2,1)$ , the output is an arrow/vector based at that point. In the vector field on the left, this output is $\left(\begin{array}{c} 3 \\ 1 \end{array}\right)$ . In the vector field on the right, this output is $\left(\begin{array}{c} 5 \\ 3\end{array}\right)$ .

Finally, we look at the vector field for Example 9. Note that all the vectors that are not on the $y$ -axis are horizontal. Also, every point on the $y$ -axis has the zero vector (a big dot) attached to it.

The transformation from Example 9, visualized as a vector field. For any point $(x,y)$ , such as $(x,y)=(2,1)$ , the output is an arrow/vector based at that point. This output is $\left(\begin{array}{c} 2 \\ 0 \end{array}\right)$ .

The transformation from Example 9, visualized as a vector field. For any point $(x,y)$ , such as $(x,y)=(2,1)$ , the output is an arrow/vector based at that point. This output is $\left(\begin{array}{c} 2 \\ 0 \end{array}\right)$ .

Relationship to the Original Geometrically-Described Mapping

It may not be clear, besides having the same formula, how these vector field pictures are related to the pictures for the original mappings. This can be made clearer with yet one more animation.

Consider Example 2, the reflection across the line $y=x$ with formula $T(x,y)=\left(\begin{array}{c} y \\ x \end{array}\right)$ . Here is the picture showing how we viewed this originally as a mapping:

To see how this is related to the vector field, we make an animation that transforms the “identity” vector field $I\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} x \\ y \end{array}\right)$ into the vector field $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} y \\ x \end{array}\right)$ . Note that each of the original vectors is being “reflected” across a $45^{\circ}$ line (colored pink) through the point at which it is based.

This animation shows how the final vector field $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} y \\ x \end{array}\right)$ (blue) can be obtained from the
‘identity’ vector field $I\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} x \\ y \end{array}\right)$ as reflections across many $45^{\circ}$ lines.

This animation shows how the final vector field $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} y \\ x \end{array}\right)$ (blue) can be obtained from the
‘identity’ vector field $I\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} x \\ y \end{array}\right)$ as reflections across many $45^{\circ}$ lines.

Relationship to Solutions of Differential Equations

In the study of differential equations, we seek solution curves which “follow” vector fields. When many of these solution curves are graphed, we get a picture of the “flow” of the vector field. The flow of the linear vector field $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} y \\ x \end{array}\right)$ is shown below.

The flow of the linear vector field $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} y \\ x \end{array}\right)$ . Compare this picture with the blue vector field from the animation directly above. Note how the curves in this flow ‘follow’ the vectors in the vector field.

We end this section by viewing two animations showing how the vector fields for the rotation $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} -y \\ x \end{array}\right)$ and the shear $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} -y \\ x \end{array}\right)$ are obtained as appropriate geometric transformations of the identity vector field $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} x \\ y \end{array}\right)$ .

Exercises

Let $f$ be a function defined by the formula $f(x)=mx+b$ for some constants $m$ and $b$ . Prove that (a) $f(u+v)=f(u)+f(v)$ and (b) $f(uv)=uf(v)$ for all $u,v\in {\Bbb R}$ if and only if $b=0$ .
Determine a formula for a transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ that maps points to their reflection across the vertical $y$ -axis. Next, prove that $T$ is linear according to the “new” definition in this section.
Determine a formula for a transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ that maps points to their reflection through the origin (so the output of a point under $T$ is another point the same distance from the origin, but in the opposite direction). Take note of the fact that this transformation is the same as a $180^{\circ}$ rotation about the origin. Next, prove that $T$ is linear according to the “new” definition in this section.
Let $a,b,c$ , and $d$ be constants. Prove that the transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ defined by $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} ax+by \\ cx+dy \end{array}\right)$ is linear.
Give a proof that the translation transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ defined by $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} x+4 \\ y-2 \end{array}\right)$ is nonlinear.
Prove that the transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ defined by $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c}x^{2} \\ -y\end{array}\right)$ is nonlinear.

Challenge Exercises

(Challenge) The parallelogram $A$ from the examples can be described in terms of two parameters (numbers) $s$ and $t$ in the following way: $A=\left\{s\left(\begin{array}{c} 4 \\ 1 \end{array}\right)+t\left(\begin{array}{c} 2 \\ 3 \end{array}\right)\, |\, 0\leq s\leq 1\mbox{ and } 0\leq t\leq 1\right\}$ . Use the linearity of the transformation $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} y \\ x \end{array}\right)$ from Example 2 to prove that $T(A)=\left\{s\left(\begin{array}{c} 1 \\ 4 \end{array}\right)+t\left(\begin{array}{c} 3 \\ 2 \end{array}\right)\, |\, 0\leq s\leq 1\mbox{ and } 0\leq t\leq 1\right\}$ .
(Challenge) Use a picture to help you explain why the transformation $T:{\Bbb R}^{2}\longrightarrow {\Bbb R}^{2}$ defined by $T\left(\begin{array}{c} x \\ y \end{array}\right)=\left(\begin{array}{c} \cos(\theta)x-\sin(\theta)y \\ \sin(\theta)x+\cos(\theta)y \end{array}\right)$ represents a counterclockwise rotation by an angle of $\theta$ about the origin.

Video for Section 1.4

Here is a video overview of the content of this section.

Visual Linear Algebra Online, Section 1.4

Linear Functions and Linear Transformations

Linear Functions in Calculus

Linear Transformations as Mappings and Vector Fields

Examples of Linear Transformations

Example 1: Reflection about the horizontal axis

Visualizing the Mapping

The Image of a Set of Points

What Makes the Reflection Linear?

What Makes This Work?

Example 2: Reflection about the line y = x

The Images of Sets of Points

What Makes the Reflection Linear?

Example 3: Expansion (Dilation) Away From the Origin

The Images of Sets of Points

Example 4: Rotation About the Origin

The Images of Sets of Points

Example 5: Shear Transformation

The Images of Sets of Points

Example 6: Translation (a Nonlinear Transformation!)

Example 7: Rotation About a Point that is Not the Origin (a Nonlinear Transformation!)

Example 8: Polar Coordinates (a “Strongly” Nonlinear Transformation)

Example 9: Projection Onto the Horizontal Axis

The Images of Sets of Points

Observations about the Examples

The Examples Reimagined as Vector Fields

Examples 1 and 2

Examples 3 and 4

Examples 5 and 6

Relationship to the Original Geometrically-Described Mapping

Relationship to Solutions of Differential Equations

Exercises

Challenge Exercises

Video for Section 1.4

Next: Section 1.5, Matrices and Linear Transformations in Low Dimensions

**Example 6: Translation (a Nonlinear Transformation!)**

**Example 7: Rotation About a Point that is Not the Origin (a Nonlinear Transformation!)**