Visual Linear Algebra Online, Section 1.8

Function composition is a fundamental binary operation that arises in all areas of mathematics. Function composition is a useful way to create new functions from simpler pieces.
When the functions are linear transformations from linear algebra, function composition can be computed via matrix multiplication.
But let’s start by looking at a simple example of function composition. Consider a spherical snowball of volume . Suppose (unrealistically) that it stays spherical as it melts at a constant rate of
. Then the volume of the snowball would be
, where
is the number of hours since it started melting and
.
How does the radius of the snowball depend on time?
Since the snowball stays spherical, we know that if is its radius, in cm, then
. This is easily solved for the radius as a function of time to get
.
Now, to find how depends on
, “compose” the functions
and
to get
. Note that we are “plugging in” the output
of the “inner” function
as input for the “outer” function
.
Schematically, if we let be the real interval domain of
, this composition might be shown like this:
.
Circle Notation and Non-Commutativity
An alternative way to write the relationship between these functions is as , or
. This “circle notation” emphasizes that function composition is a binary operation. The small circle
represents the operation of taking two functions
and
and forming one new function
.
Unlike addition or multiplication of numbers, however, composition of functions is not commutative. In general, .
This inequality is certainly the case in our example.
Ignoring the fact that the reverse composition makes no physical sense for this application, we also get a completely different function: .
The key distinction here when comparing this function with is not that the variable name is different. Rather, it is that the arithmetic operations that the functions represent are different. For most given inputs, the corresponding outputs of these functions are different. Their graphs are also different.
Composing Linear Functions from Precalculus and Calculus
Function composition usually produces a different type of function from the original functions. An exception to this general rule arises with linear functions.
Suppose we consider two linear functions of the type you have encountered before linear algebra, say and
. Then
and
are both linear.
According to our new definition of linearity in linear algebra, we might therefore wonder: is the composition of two linear transformations also a linear transformation?
Composing Linear Transformations
Let and
be positive integers. Suppose
and
be linear transformations. Is the composition
also a linear transformation?
To find out, suppose and
. We can use the definition of linearity found in Section 1.7, “High-Dimensional Linear Algebra” to do the computation below. Notice the importance of the assumption that
and
are both linear in this computation.
But how is this linearity related to the matrix representatives of these linear transformations? We might start investigating the answer to this question by considering examples in low dimensions.
Before doing so, it is important to recall that we have already defined a matrix times a vector in Section 1.7, “High-Dimensional Linear Algebra”. Specifically, if is an
matrix (
rows and
columns) and
is an
-dimensional vector (an
matrix), then the matrix/vector product
will be an
-dimensional vector (an
matrix). Even more specifically,
will be the
-dimensional vector formed as a linear combination of the columns of
with the entries of
as the corresponding weights.
In a formula, if , where the
are the columns of
, and if
, then:
.
Matrix Multiplication for a Composition 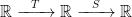
Suppose and
are linear transformations. Then there are constants (
matrices)
and
such that
and
for all
.
The composition of these functions is . In other words, the
matrix (number) corresponding to the composition is the product of the
matrices (numbers) corresponding to each of the “factors”
and
of
.
This leads us to define the product of matrices as another
matrix:
. Matrix multiplication is easy when the matrices are
. Just multiply the numbers!
Matrix Multiplication for a Composition 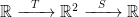
Suppose and
are linear transformations. Then there is a
matrix
and a
matrix
such that
for all
and
for all
.
We seek to define the matrix product in such a way that
for all
. Doing so in this situation necessarily implies that the product
must be a
matrix (a number).
If and
, then we can write the equations below.
, and
.
The composed function is therefore:
Notice that the final answer is the same as the following matrix product of matrices (numbers)
Therefore, the matrix product should be the
matrix below. This illustrates that a
matrix times a
matrix can be defined and the answer is a
matrix.
Since is really a two-dimensional (column) vector, we have already done this computation before! The answer is a linear combination of the columns of
with the entries of
as the weights.
Matrix Multiplication for a Composition 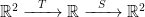
Suppose and
are linear transformations. Then there is a
matrix
and a
matrix
such that
for all
and
for all
.
We seek to define the matrix product in such a way that
for all
. Doing so in this situation necessarily implies that the product
must be a
matrix.
If and
, then we can write the equations below.
, and
.
The composed function is therefore:
.
This can be rewritten as:
.
By our previous definition of matrix/vector multiplication, this is the same as saying that
.
Therefore, to define matrix multiplication of a matrix times a
matrix, we should do it as shown below:
.
This is a fundamentally new kind of product from what we have done before. However, notice that it can be written in the following way, where each column of the answer is a two-dimensional vector formed by as the matrix
times a
column from
.
This pattern will work in the general case which we will soon specify.
Matrix Multiplication for a Composition 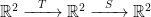
One more example in low dimensions will be considered before we discuss the general case.
Suppose and
are linear transformations. Then there is a
matrix
and a
matrix
such that
for all
and
for all
.
Once again, we seek to define the matrix product in such a way that
for all
. Doing so in this situation necessarily implies that the product
must be a
matrix.
If and
, then we can write the equations below.
,
and
.
The composed function is therefore:
,
which equals
.
By our definition of matrix/vector multiplication, this is the same thing as
.
Therefore, we define the matrix multiplication of two
matrices to be the same
matrix as on the previous line. Specifically,
.
Notice that if and
are the columns of
, then
and
are the columns of
.
Thus,
.
This is again the pattern that we will see in the general case.
Matrix Multiplication for The General Case 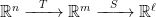
The reasoning in the general case is probably more interesting and enlightening, though it does take intense concentration to fully understand.
Suppose and
are linear transformations. Then there is a
matrix
and a
matrix
such that
for all
and
for all
.
Once again, we seek to define the matrix product in such a way that
for all
. Doing so in this situation necessarily implies that the product
must be a
matrix.
Suppose , where each
, and suppose
.
We already know that .
Since is linear and
, we can also say:
But this is a linear combination of the -dimensional vectors
with the entries of
as the weights!
In other words,
.
If this is to equal , we should define the matrix product
to be the following
matrix:
.
This is indeed what we do.
Alternative Approach with Dot Products
Of course, this means each column of is a linear combination of the columns of
with entries from the appropriate column of
as the corresponding weights.
To be more precise, let , where each column is a vector in
. Furthermore, let
be the
column of
, for
. Then the
column of
is
.
Let be the entry in the
row and
column of the product
(with
and
). Furthermore, for
, let
be the
column of
.
What we have done also shows that, for and
,
.
It is very much worth noticing that is a dot product. It is a dot product of the
column
of
with the
row of
(which we can certainly think of as a vector).
This description of the entries of as dot products is actually a quicker way to find
. It is less meaningful as a definition, however.
Our approach with linear transformations gets at the heart of the true meaning of the matrix multiplication : it should be directly related to composite linear transformations.
The Dimensions of the Matrix Factors of the Product
It is important to note that the product of an
matrix
(on the left) times an
matrix
(on the right) can be done, and that the answer is a
matrix.
That is, the number of columns of must match the number of rows of
. Furthermore, the final answer has the same number of rows as
and the same number of columns as
.
Because of this, you should also realize that just because the product can be computed, this does not mean the reverse product
can be computed.
When is
and
is
, the reverse product
can be computed if and only if
. However, even in this situation, it is usually the case that
. This reflects the fact that function composition is not commutative in general either.
The Associative Property of Matrix Multiplication
Before considering examples, it is worth emphasizing that matrix multiplication satisfies the associative property. This reflects the fact that function composition is associative.
Suppose ,
, and
are all linear transformations. Then the equation
is easy to verify.
Given an arbitrary , we have
If ,
, and
for appropriately sized matrices and variable vectors, then the equation
will clearly hold as well.
The associative property generalizes to any matrix product with a finite number of factors. It also implies that can write such products without using parentheses.
Example 1
We will first consider a purely computational high-dimensional example. After this point, we will consider low-dimensional examples that can be visualized.
Define and
by the following formulas.
and
Then is defined by
, where
.
Now compute each column individually. We will do the first column.
etcetera.
You should definitely take the time to check that the final matrix product is
.
We can also double-check this by using the dot product as described above.
For example, consider , the entry in the third row and second column of the product
. The third row of
is
, while the second column of
is
. The dot product of these two vectors is
.
Therefore, the final formula for the composite linear transformation is
.
Of course, now that we know the matrix for the composition , we can use elementary row operations to, for example, determine its kernel (null space).
As an exercise, you should take the time to show that the augmented matrix for the system can be reduced to the shown reduced row echelon form (RREF).
Therefore and
are free variables and the kernel (null space) is a two-dimensional plane through the origin in five-dimensional space.
Example 2
The next two examples are two-dimensional so that we can easily visualize them. For the purpose of reviewing Section 1.4, “Linear Transformations in Two Dimensions”, we emphasize visualizing a linear transformation both as a mapping and as a vector field.
What happens when we compose a rotation and a shear, for example?
We explore that now. We will use a different set of letters for the transformation names to avoid confusion with their geometric effects.
Suppose and
be defined by
and
.
Then is the shear transformation discussed in Section 1.4, “Linear Transformations in Two Dimensions” and
is a rotation transformation counterclockwise around the origin by
.
The matrix product will define the formula for the composite transformation
. On the other hand, the matrix product
will define the formula for the composite transformation
.
Let’s compute formulas for both functions. We will use the equivalent dot product formulation of matrix multiplication.
.
For the reverse composition, to be consistent with what we have done so far, we use y‘s for the variable names. Don’t let this bother you. We could have used x‘s.
.
These two transformations are indeed different. That is, . This should be expected. Function composition is not commutative.
Matrix multiplication is also not commutative, even when both and
can be computed.
Visualizing the Compositions as Mappings
Can the geometric effects of these compositions be easily visualized? Yes, but they are not “simple” visualizations. Essentially it is best to look at their geometric effects in the order that they occur.
Here is a visual that shows how these two different compositions each affect the butterfly curve from Section 1.4, “Linear Transformations in Two Dimensions”. In each case, the beginning (red) butterfly represents a set of points that will be transformed under the composite mapping to the ending (blue) butterfly. The ending butterfly is the image of the composite map
(on the left) and
(on the right), respectively.

Visualizing the Compositions as Vector Fields
Recall that a vector field representation of a linear transformation takes each point
as input and “attaches” the output vector to this point as an arrow.
As static pictures, these vector fields are shown below.

We can animate this as well to see the connection with the mapping view of the linear transformation. We can see the “shearing” and “rotating” in each case if we imagine transforming each vector in the vector field from the “identity” vector field .
In each case, the starting (identity) vector field is red, the intermediate vector field is purple, and the final vector field is blue.

Example 3
For our final example, we consider the composition of two reflections. One transformation will be a reflection across the horizontal axis. The other transformation will be a reflection across the diagonal line through the origin.
We will call these reflections and
(“h” for horizontal and “d” for diagonal). We will also write
and
for some
matrices
and
and
.
The formula for based on the matrix product
is this:
.
And the formula for based on the matrix product
is this:
.
Visualizations
Let be arbitrary. Note that
. On the other hand, we can say that
. This is a very special property.
We should see this reflected in our animations (pun intended).

Here are the static vector fields.

And here are the animations of the identity vector field being transformed into each of these vector fields. Notice how the starting vectors (red) are getting reflected to the intermediate state (purple) before going on to the final state (blue).

Exercises
- Let
and
. Find and simplify formulas for
and
. Note that the results are different functions.
- Let
and
. (a) Find and simplify formulas for
and
. Note that the results are different functions. Note however, in this situation, that both (simplified) functions are of the “same type” as the originals. When the inputs are allowed to be complex numbers, such functions are called linear fractional transformations. As mappings of the complex plane, they have a number of beautiful properties that are worth investigating.
- Let
and
. (a) Find the product
. (b) Let
and
be defined by
and
, for
and
. Find a simplified formula for
. (c) Find the kernel of
.
Video for Section 1.8
Here is a video overview of the content of this section.
