Integration by Substitution (Method of Integration)

Calculus 2, Lectures 2A through 3A (Videotaped Fall 2016)

How to visualize integration by substitution for a definite integral. The starting and ending areas are the same. — The integral $\displaystyle\int_{0}^{\sqrt{\pi/2}}2x\cos(x^{2})\, dx$ gets transformed to the integral $\displaystyle\int_{0}^{\pi/2}\cos(u)\, du$ under the substitution $u=x^{2}$ and $du=2xdx$ .

The integral $\displaystyle\int_{0}^{\sqrt{\pi/2}}2x\cos(x^{2})\, dx$ gets transformed to the integral $\displaystyle\int_{0}^{\pi/2}\cos(u)\, du$ under the substitution $u=x^{2}$ and $du=2xdx$ .

In Calculus 1, the techniques of integration introduced are usually pretty straightforward. In fact, they are usually just memorized as basic facts about antiderivatives.

For Calculus 2, various new integration techniques are introduced, including integration by substitution. That is the main subject of this blog post.

Other techniques we will look at in later posts for this series on Calculus 2 are: 1) integration by parts, 2) trigonometric substitutions, 3) the method of partial fractions, 4) the use of appropriate trigonometric identities, and 5) tables and technology.

Educated Guessing for Relatively Simple Integrals

For simpler problems, integration by substitution can be thought of as “educated guessing”.

For example, what is the most general antiderivative of $f(x)=e^{2x}$ ? Notationally, we write this problem using an indefinite integral sign: Find $\displaystyle\int e^{2x}\, dx$ .

If this problem were to find $\displaystyle\int e^{x}\, dx$ instead, the answer would be straightforward. It’s based on memorization: Since $\frac{d}{dx}\left(e^{x}\right)=e^{x}$ , it follows that $\displaystyle\int e^{x}\, dx=e^{x}+C$ (don’t forget to add the +C for the most general antiderivative).

But the “2” in $e^{2x}$ makes the integral $\displaystyle\int e^{2x}\, dx$ more difficult. Can we “replace” or “substitute” $2x$ with something simpler, such as a $u$ ? The answer is “yes”, but “adjustments” have to be made.

Think of it in terms of differentiation. The Chain Rule implies that $\frac{d}{dx}\left(e^{2x}\right)=2e^{2x}$ . Moreover, the linearity of the derivative operator $\frac{d}{dx}$ implies that $\frac{d}{dx}\left(\frac{1}{2}e^{2x}\right)=\frac{1}{2}\cdot \frac{d}{dx}\left(e^{2x}\right)=\frac{1}{2}\cdot (2e^{2x})=e^{2x}$ . Therefore, $\displaystyle\int e^{2x}\, dx=\frac{1}{2}e^{2x}+C$ .

Thinking of This in Terms of a New Variable (the “Substitution”)

The Chain Rule itself can be thought of in terms of substitution. Consider the function $y=f(x)=e^{2x}$ again. This function can be thought of as a function composition of two simpler functions. If $u=h(x)=2x$ and $y=g(u)=e^{u}$ , then $y=f(x)=g(h(x))=(g\circ h)(x)$ .

In this context, the Chain Rule can be written in two ways: either as 1) $\frac{dy}{dx}=f'(x)=g'(h(x))\cdot h'(x)$ , or as 2) $\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx}$ .

The second way works out like this: Since $\frac{dy}{du}=e^{u}$ and $\frac{du}{dx}=2$ , we can write $\frac{dy}{dx}=e^{u}\cdot 2=2e^{2x}$ because $u=2x$ .

Returning to integration, we could then write

$\displaystyle\int y\, dx=\displaystyle\int e^{2x}\, dx=\displaystyle\int e^{u}\, dx$ .

But if we are going to finish this integral, we need to use the fact that $dx$ depends on $du$ .

Since $\frac{du}{dx}=2$ , we can informally imagine “multiplying” both sides of this equation by $dx$ to get $du=2dx$ . Then, divide both sides by $2$ to get $dx=\frac{1}{2}du$ . This means that:

$\displaystyle\int e^{u}\, dx=\displaystyle\int \frac{1}{2}e^{u}\, du=\frac{1}{2}e^{u}+C\ \ \ (\mbox{Note: } dx=\frac{1}{2}du)$ .

This is just an intuitive approach involving infinitesimals that will lead us to the right answer below. It is not a rigorous justification, though it can be checked by differentiation.

We want our final answer to depend on the original variable $x$ , so make the replacement $u=2x$ . The final answer is

$\displaystyle\int e^{2x}\, dx=\frac{1}{2}e^{2x}+C$ .

As was already emphasized, here is an extremely important point: You can always check the answer by differentiation!

In this case, $\frac{d}{dx}\left(\frac{1}{2}e^{2x}+C\right)=\frac{1}{2}e^{2x}\cdot 2+0=e^{2x}$ .

A Couple More Basic Examples of Integration by Substitution

Consider $\displaystyle\int 3\cos(5x)\, dx$ . If this problem were $\displaystyle\int 3\cos(u)\, du$ instead, the answer would be $3\sin(u)+C$ .

Because of this, we are inspired to define the substitution $u=5x$ .

But remember, we must also find how $dx$ depends on $du$ . Since $u=5x$ , we can write $\frac{du}{dx}=5$ so that $du=5dx$ and $dx=\frac{1}{5}du$ . In fact, we can also multiply both sides by 3 to get $3dx=\frac{3}{5}du$ .

Hence,

$\displaystyle\int 3\cos(5x)\, dx=\displaystyle\int \frac{3}{5}\cos(u)\, du=\frac{3}{5}\sin(u)+C=\frac{3}{5}\sin(5x)+C$ .

Don’t forget to check by differentiation, once again, using the Chain Rule. This gives $\frac{d}{dx}\left(\frac{3}{5}\sin(5x)+C\right)=\frac{3}{5}\cos(5x)\cdot 5+0=3\cos(3x)$ , which is the original integrand (the function to be integrated).

The answer is correct!

Here’s another basic example, though it appears to be more difficult: Compute $\displaystyle\int 3x^{2}(x^{3}+5)^{10}\, dx$ .

While this problem is possible to do without substitution, it is very unpleasant to do so because you have to expand out $(x^{3}+5)^{10}$ using the binomial theorem (possibly with the help of Pascal’s triangle).

But, we are “lucky” in this problem. The fact that $\frac{d}{dx}\left(x^{3}+5\right)=3x^{2}$ helps us to see that the substitution $u=x^{3}+5$ is the best choice to make. Then $du=3x^{2}dx$ and we can write

$\displaystyle\int 3x^{2}(x^{3}+5)^{10}\, dx=\displaystyle\int u^{10}\, du=\frac{1}{11}u^{11}+C=\frac{1}{11}(x^{3}+5)^{11}+C$ .

Differentiate this answer to confirm that it is correct!

Lecture 2A: Integration by Substitution, Including for a Definite Integral

After some preliminaries, I begin Lecture 2A with an example similar to the preceding one. Next, I move on to a trickier-looking example: Find $\displaystyle\int \frac{\sin(\sqrt{x})}{\sqrt{x}}\, dx$ .

Calculus 2, Lecture 2A: Integration by Substitution Examples, Check with the Chain Rule

Even though this integral looks impossible, we are actually “lucky” again. If you just try the substitution $w=\sqrt{x}$ , you will be rewarded with success (note that it does not matter what we call the “new” variable — $u$ and $w$ are the most common choices).

Why? Because then $\frac{dw}{dx}=\frac{1}{2}x^{-1/2}$ , so that $2dw=\frac{1}{\sqrt{x}}\, dx$ . And this allows us to write $\displaystyle\int \frac{\sin(\sqrt{x})}{\sqrt{x}}\, dx=\displaystyle\int 2\sin(w)\, dw$ .

Doing this last integral is easy. The answer, based on memorization, is $-2\cos(w)+C$ . Therefore, $\displaystyle\int \frac{\sin(\sqrt{x})}{\sqrt{x}}\, dx=-2\cos(\sqrt{x})+C$ .

Once again, this can be checked with the Chain Rule and Linearity. Doing this gives:

$\frac{d}{dx}\left(-2\cos(\sqrt{x})+C\right)=2\sin(\sqrt{x})\cdot \frac{d}{dx}(\sqrt{x})=2\sin(\sqrt{x})\cdot \frac{1}{2}x^{-1/2}=\frac{\sin(\sqrt{x})}{\sqrt{x}}.$

It works!

When and Why Does Integration by Substitution Work?

Integration by substitution works for indefinite integrals of the form $\displaystyle\int k f(g(x))g'(x)\, dx$ for some constant $k$ .

For example, in the last problem, we can write $\displaystyle\int \frac{\sin(\sqrt{x})}{\sqrt{x}}\, dx=\displaystyle\int 2\sin(\sqrt{x})\cdot \frac{1}{2}x^{-1/2}\, dx$ . This helps us see that $k=2$ , $f(u)=\sin(u)$ (going back to using $u$ again), and $g(x)=\sqrt{x}$ , so that $f(g(x))=\sin(\sqrt{x})$ and $g'(x)=\frac{1}{2}x^{-1/2}$ .

In the general setting of the integral $\displaystyle\int k f(g(x))g'(x)\, dx$ , we let $u=g(x)$ so that $\frac{du}{dx}=g'(x)$ and $du=g'(x)\, dx$ . Then we can write $\displaystyle\int k f(g(x))g'(x)\, dx=\displaystyle\int kf(u)\, du$ .

If $F(u)$ is an antiderivative of $f(u)$ , then $\displaystyle\int kf(u)\, du=kF(u)+C$ . The original integral is then $\displaystyle\int k f(g(x))g'(x)\, dx=kF(g(x))+C$ .

This can be checked by the Chain Rule and Linearity once again. Since $F'(u)=f(u)$ for all $u$ , we get

$\frac{d}{dx}\left(kF(g(x))+C\right)=kF'(g(x))\cdot g'(x)=kf(g(x))g'(x)$ .

This helps us see why the Chain Rule is always necessary when checking an integration by substitution problem. Integration by substitution is really the “inverse method” of the Chain Rule for differentiation.

Doing a Definite Integral using Integration by Substitution

Also in Lecture 2A, I do the following definite integral: $\displaystyle\int_{1}^{2}x^{3}e^{x^{4}}\, dx$ .

This can be done in one of two ways:

Find an antiderivative of the integrand $x^{3}e^{x^{4}}$ first (using substitution) and then use the Fundamental Theorem of Calculus (FTC), or
Use a substitution and the FTC to find both an antiderivative and the definite integral at the “same time”. Do not go back to using the original variable $x$ when this method is used.

It is worthwhile to try both methods and to see that we get the same answer.

The substitution is the same for both methods: $u=x^{4}$ so that $du=4x^{3}dx$ and $\frac{1}{4}du=x^{3}dx$ .

Then $\displaystyle\int x^{3}e^{x^{4}}\, dx=\displaystyle\int\frac{1}{4}e^{u}\, du=\frac{1}{4}e^{u}+C=\frac{1}{4}e^{x^{4}}+C$ . Hence, Method 1 and the FTC give

$\displaystyle\int_{1}^{2}x^{3}e^{x^{4}}\, dx=\frac{1}{4}e^{2^{4}}-\frac{1}{4}e^{1^{4}}=\frac{1}{4}(e^{16}-e)$ .

On the other hand, if we use Method 2, we must change the limits of integration.

Why? We will explore the reasons in the next section below.

For the moment, note that since $x$ varies from 1 to 2 in the original definite integral and $u=x^{4}$ , it follows that $u$ varies from $1^{4}=1$ to $2^{4}=16$ in the “new” definite integral.

This means is that

$\displaystyle\int_{1}^{2}x^{3}e^{x^{4}}\, dx=\displaystyle\int_{1}^{16}\frac{1}{4}e^{u}\, du=\frac{1}{4}e^{16}-\frac{1}{4}e^{1}=\frac{1}{4}(e^{16}-e)$ .

We do indeed get the same answer as before!

Why Does Method 2 Work?

The definite integral we solved above has the form $\displaystyle\int_{a}^{b} k f(g(x))g'(x)\, dx$ for some constant $k$ . If we let $u=g(x)$ so that $du=g'(x)\, dx$ as before, then doing a substitution and changing the limits of integration as above gives the definite integral $\displaystyle\int_{g(a)}^{g(b)}kf(u)\, du$ .

Suppose $F$ is an antiderivative of $f$ for all possible inputs. Then the Fundamental Theorem of Calculus (FTC) implies that

$\displaystyle\int_{g(a)}^{g(b)}kf(u)\, du=k\displaystyle\int_{g(a)}^{g(b)}f(u)\, du=kF(g(b))-kF(g(a))$ .

But wait! By the Chain Rule and Linearity, we know that $\frac{d}{dx}\left(kF(g(x))\right)=kF'(g(x))\cdot g'(x)=kf(g(x))g'(x)$ . This means that the composite function $kF(g(x))$ is an antiderivative of $kf(g(x))g'(x)$ .

Applying the FTC once again shows that

$\displaystyle\int_{a}^{b} k f(g(x))g'(x)\, dx=kF(g(b))-kF(g(a))$ .

But this is the same result that we got before! In other words,

$\displaystyle\int_{a}^{b} k f(g(x))g'(x)\, dx=\displaystyle\int_{g(a)}^{g(b)}kf(u)\, du$ .

This is the symbolic reason why substitution Method 2 works for definite integrals.

Visualizing Method 2

Method 2 is tough to explain from an intuitive point of view. You almost have to just rely on your understanding of the symbols and your trust in the theorems.

However, Method 2 can still be visualized.

Consider another example. Suppose we wish to find the value of $\displaystyle\int_{0}^{\sqrt{\pi/2}}2x\cos(x^{2})\, dx$ . We use Method 2 with the substitution $u=x^{2}$ and $du=2x\, dx$ to get

$\displaystyle\int_{0}^{\sqrt{\pi/2}}2x\cos(x^{2})\, dx=\displaystyle\int_{0}^{\pi/2}\cos(u)\, du=\sin(\pi/2)-\sin(0)=1$ .

Geometrically, since both functions are non-negative over the respective intervals, this means that the area under the graph of the function $2x\cos(x^{2})$ as $x$ varies from 0 to $\sqrt{\pi/2}\approx 1.253$ and the area under the graph of the function $\cos(u)$ as $u$ varies from 0 to $\pi/2\approx 1.571$ are both equal to 1.

If we imagine the substitution $u=x^{2}$ as a (nonlinear) transformation, then we can imagine the area under the first graph getting transformed to the area under the second graph as shown below.

Animation to illustrate how integration by substitution works for a definite integral example. The area under the starting graph and the ending graph are the same, and they are both equal to one. — Visual for the substitution $u=x^{2}$ which shows that $\displaystyle\int_{0}^{\sqrt{\pi/2}}2x\cos(x^{2})\, dx=\displaystyle\int_{0}^{\pi/2}\cos(u)\, du$ . The areas under these graphs over the appropriate intervals are both equal to 1. Since each box has an area of $0.25^{2}=0.04$ , this means there are 25 boxes (including partial boxes) under both the beginning and ending graphs.

Visual for the substitution $u=x^{2}$ which shows that $\displaystyle\int_{0}^{\sqrt{\pi/2}}2x\cos(x^{2})\, dx=\displaystyle\int_{0}^{\pi/2}\cos(u)\, du$ . The areas under these graphs over the appropriate intervals are both equal to 1. Since each box has an area of $0.25^{2}=0.04$ , this means there are 25 boxes (including partial boxes) under both the beginning and ending graphs.

Lectures 2B and 3A: Introduction to Applications of Integration and More Integration by Substitution Examples

Lecture 2B: Broad Overview of Integral Applications and Mathematica Usage

In Lecture 2B, I introduce the following applications of definite integrals:

Integrate the velocity function of an object (a “particle”) to find its change in position.
Integrate the difference of two functions to find the area of the region between their graphs (which has real-life applications as well).
Compute the integral of a function over an interval and divide by the length of the interval to find the average value of a function (which has real-life applications as well).
Integrate the probability density function (PDF) for a continuous random variable over an interval $[a,b]$ to find the probability that the variable takes on a value in the interval $[a,b]$ .

Calculus 2, Lecture 2B: Broad Overview of Integral Applications and Mathematica Usage

I will go into details about these applications in later blog posts of this series.

But, for the moment, let me remark that the example I chose in Lecture 2B for finding the area between two curves was a poor example. And let me rectify that bad choice by doing a better example here.

Example: Find the area between the parabolas 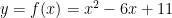$y=f(x)=x^{2}-6x+11$ and $y=g(x)=-x^{2}+4x+3$

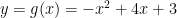
Here is a picture of the region whose area we want to find.

Find the area of the region between two parabolas. — Find the area of the region bounded by the graphs of the functions $y=f(x)=x^{2}-6x+11$ and $y=g(x)=-x^{2}+4x+3$ . This is a region bounded by two parabolas.

Find the area of the region bounded by the graphs of the functions $y=f(x)=x^{2}-6x+11$ and $y=g(x)=-x^{2}+4x+3$ . This is a region bounded by two parabolas.

From the picture, it appears that the curves intersect at $x=1$ and $x=4$ .

We should confirm this with algebra. Set $f(x)=g(x)$ and solve for $x$ . We get $x^{2}-6x+11=-x^{2}+4x+3$ , which is equivalent to $2x^{2}-10x+8=0$ . This can be solved with the quadratic formula. It can also be factored:

$0=2x^{2}-10x+8=2(x^{2}-5x+4)=2(x-1)(x-4)$

From this, we see that the solutions are $x=1$ and $x=4$ .

Since the function $g(x)$ is “on the top” and the function $f(x)$ is “on the bottom” of the region, it is clear that the difference of the integrals $\displaystyle\int_{1}^{4}g(x)\, dx-\displaystyle\int_{1}^{4}f(x)\, dx$ is the area we seek.

By linearity of integration, this is the same as the integral of the difference $g(x)-f(x)=-2x^{2}+10x-8$ over the same interval. Since an antiderivative of this is $h(x)=-\frac{2}{3}x^{3}+5x^{2}-8x$ , the Fundamental Theorem of Calculus implies that

$\mbox{Area}=\displaystyle\int_{1}^{4}\left(-2x^{2}+10x-8\right)dx=h(4)-h(1)=\frac{16}{3}-\left(-\frac{11}{3}\right)=\frac{27}{3}=9$ .

Since the area of each “box” in the picture above is $1\times 2=2$ units, this should seem reasonable.

Lecture 3A: Inflow and Outflow, Probability, Tricky Substitution Problems

In Lecture 3A, I continue discussing applications. The applications are to inflow and outflow of water in a tank, as well as a review of probability density functions from Lecture 2B. As stated earlier, we will look at these and other applications in more depth in later blog posts.

Calculus 2, Lecture 3A: Inflow and Outflow, Probability, Tricky Substitution Problems

After that, I finish Lecture 3A by doing two tricky integration by substitution problems. I will end this blog post by showing you how to solve these problems.

Two Tricky Integration by Substitution Problems

Example 1: Find 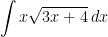$\displaystyle\int x\sqrt{3x+4}\, dx$

Why is this problem tricky? The reason is that it does not seem to be of the form $\displaystyle\int kf(g(x))g'(x)\, dx$ .

Why not? If we try letting $u=g(x)=3x+4$ , then $du=g'(x)dx=3dx$ . But what do we do with the extra $x$ in the integrand function $x\sqrt{3x+4}$ ?

Don’t give up! Just keep going!

Try the only thing you can do: if $u=3x+4$ , then $3x=u-4$ and $x=\frac{1}{3}u-\frac{4}{3}$ .

Also, $dx=\frac{1}{3}du$ , so $\displaystyle\int x\sqrt{3x+4}\, dx=\displaystyle\int \left(\frac{1}{3}u-\frac{4}{3}\right)\sqrt{u}\cdot \frac{1}{3}\, du$ .

Is this helpful? Yes! Expand out the integrand like this:

$\displaystyle\int x\sqrt{3x+4}\, dx=\displaystyle\int \left(\frac{1}{9}u^{3/2}-\frac{4}{9}u^{1/2}\right)\, du$ .

Now you can finish the problem using the fact that $\displaystyle\int u^{n}\, du=\frac{u^{n+1}}{n+1}+C$ when $n\not=-1$ .

$\displaystyle\int \left(\frac{1}{9}u^{3/2}-\frac{4}{9}u^{1/2}\right)\, du=\frac{2}{45}u^{5/2}-\frac{8}{27}u^{3/2}+C$ .

Therefore,

$\displaystyle\int x\sqrt{3x+4}\, dx=\frac{2}{45}(3x+4)^{5/2}-\frac{8}{27}(3x+4)^{3/2}+C$ .

This can be checked with the Chain Rule along with a bit of algebra:

$\frac{d}{dx}\left(\frac{2}{45}(3x+4)^{5/2}-\frac{8}{27}(3x+4)^{3/2}\right)=\frac{1}{3}(3x+4)^{3/2}-\frac{4}{3}(3x+4)^{1/2}$

$=\sqrt{3x+4}\left(\frac{1}{3}(3x+4)-\frac{4}{3}\right)=\sqrt{3x+4}\left(x+\frac{4}{3}-\frac{4}{3}\right)=x\sqrt{3x+4}$ .

Example 2: Find $\displaystyle\int_{0}^{9} \frac{1}{5+8\sqrt{x}}\, dx$

This example seems to have the same difficulty as the previous one. The integrand function $\frac{1}{5+8\sqrt{x}}$ also does not appear to be of the form $kf(g(x))g'(x)$ .

But, once again, sometimes you just need to try something and see what happens. It seems that one possible choice for a substitution to try is $u=5+8\sqrt{x}$ .

If we do this, then $du=4x^{-1/2}dx=\frac{4}{\sqrt{x}}dx$ . This implies that $dx=\frac{1}{4}\sqrt{x}du$ .

Is this helpful? Solve $u=5+8\sqrt{x}$ for $\sqrt{x}$ to get $\sqrt{x}=\frac{u-5}{8}=\frac{1}{8}u-\frac{5}{8}$ . Then $dx=\left(\frac{1}{32}u-\frac{5}{32}\right)du$ .

Also, when $x=0$ , we get $u=5+8\sqrt{0}=5$ and when $x=9$ , we get $u=5+8\sqrt{9}=29$ .

This implies that we can now write $\displaystyle\int_{0}^{9} \frac{1}{5+8\sqrt{x}}\, dx=\displaystyle\int_{5}^{29}\frac{1}{u}\left(\frac{1}{32}u-\frac{5}{32}\right)du$ .

We are in luck! This integral is definitely do-able!

$\displaystyle\int_{5}^{29}\frac{1}{u}\left(\frac{1}{32}u-\frac{5}{32}\right)du=\displaystyle\int_{5}^{29}\left(\frac{1}{32}-\frac{5}{32u}\right)du=\frac{1}{32}u-\frac{5}{32}\ln|u|\biggr\rvert_{5}^{29}$ .